Question

【题目】已知抛物线与轴交于，两点，顶点为，如果为直角三角形，则________.

Answer 1

【答案】

【解析】

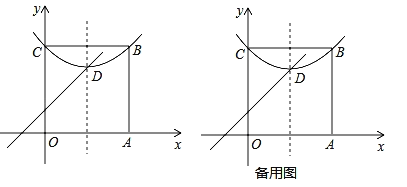
抛物线y=ax2-x-1与x轴交于A，B两点，顶点为C，△ABC为直角三角形，根据对称性可知，△ABC必是等腰直角三角形，于是有与x轴两个交点之间的距离等于顶点到x轴距离的2倍，分别表示出这两个距离，列方程求解，检验得出答案．

解：∵抛物线y=ax2-x-1与x轴交于A，B两点，
∴b2-4ac＞0，

即1+4a＞0，也就是

∵抛物线y=ax2-x-1与x轴交点的横坐标为，顶点的纵坐标为，

∴AB的距离为|x1-x2|= 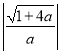，顶点C到x轴距离CD为，

∵当△ABC为直角三角形，根据对称性可知它是一个等腰直角三角形，此时AB=2CD，

于是：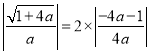

两边平方得：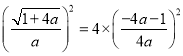

整理得：16a2-8a-3=0
解得：

∵

∴