题目内容
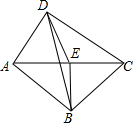 如图,将两块直角三角板的斜边重合,E是两直角三角形公共斜边AC的中点.D、B分别为直角顶点,连接DE、BE、DB,∠DAC=60°,∠BAC=45°.则∠EDB的度数为________.
如图,将两块直角三角板的斜边重合,E是两直角三角形公共斜边AC的中点.D、B分别为直角顶点,连接DE、BE、DB,∠DAC=60°,∠BAC=45°.则∠EDB的度数为________.
15°
分析:根据三角形内角和定理求出∠ADB+∠ABD=75°,根据直角三角形斜边上中线求出DE=BE,推出∠EDB=∠EBD,求出∠EDB+∠EBD,即可求出答案.
解答:∵∠DAC=60°,∠BAC=45°,
∴∠DAB=105°,
∴∠ADB+∠ABD=180°-105°=75°,
∵△ADC和△ABC中,∠ADC=∠ABC=90°,E为斜边AC的中点,
∴DE=AE= AC,BE=AE=
AC,BE=AE= AC,
AC,
∴DE=BE,∠EDA=∠DAC=60°,∠EBA=∠BAC=45°,
∴∠EDB+∠EBD=(60°+45°)-75°=30°,
∵DE=BE,
∴∠EDB=∠EBD=15°,
故答案为:15°.
点评:本题考查了三角形的内角和定理,直角三角形斜边上中线,等腰三角形的性质和判定等知识点,关键是求出∠EDB+∠EBD的度数和推出DE=BE.
分析:根据三角形内角和定理求出∠ADB+∠ABD=75°,根据直角三角形斜边上中线求出DE=BE,推出∠EDB=∠EBD,求出∠EDB+∠EBD,即可求出答案.
解答:∵∠DAC=60°,∠BAC=45°,
∴∠DAB=105°,
∴∠ADB+∠ABD=180°-105°=75°,
∵△ADC和△ABC中,∠ADC=∠ABC=90°,E为斜边AC的中点,
∴DE=AE=
 AC,BE=AE=
AC,BE=AE= AC,
AC,∴DE=BE,∠EDA=∠DAC=60°,∠EBA=∠BAC=45°,
∴∠EDB+∠EBD=(60°+45°)-75°=30°,
∵DE=BE,
∴∠EDB=∠EBD=15°,
故答案为:15°.
点评:本题考查了三角形的内角和定理,直角三角形斜边上中线,等腰三角形的性质和判定等知识点,关键是求出∠EDB+∠EBD的度数和推出DE=BE.

练习册系列答案
相关题目
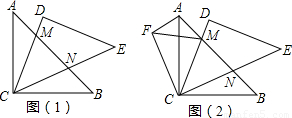
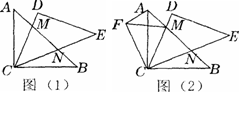
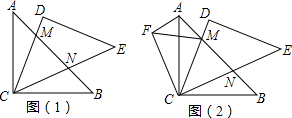 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由. 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.