题目内容
在半径为2a的⊙O中,弦AB长为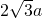 ,则∠AOB为
,则∠AOB为
- A.90°
- B.120°
- C.135°
- D.150°
B
分析:作弦的弦心距OC,首先根据垂径定理,得半弦是 a;根据锐角三角函数定义,得∠AOC=60°.
a;根据锐角三角函数定义,得∠AOC=60°.
再根据等腰三角形的三线合一,得∠AOB=120°.
解答: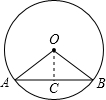 解:如图,作弦心距OC,则有AO=2a,AC=
解:如图,作弦心距OC,则有AO=2a,AC= a.
a.
sin∠AOC=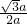 =
= .
.
∴∠AOC=60°,
∴∠AOB=2∠AOC=120°.
故选B.
点评:此题综合运用了垂径定理、锐角三角函数根据边的关系计算角的度数、等腰三角形的三线合一.
分析:作弦的弦心距OC,首先根据垂径定理,得半弦是
 a;根据锐角三角函数定义,得∠AOC=60°.
a;根据锐角三角函数定义,得∠AOC=60°.再根据等腰三角形的三线合一,得∠AOB=120°.
解答:
 解:如图,作弦心距OC,则有AO=2a,AC=
解:如图,作弦心距OC,则有AO=2a,AC= a.
a.sin∠AOC=
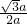 =
= .
.∴∠AOC=60°,
∴∠AOB=2∠AOC=120°.
故选B.
点评:此题综合运用了垂径定理、锐角三角函数根据边的关系计算角的度数、等腰三角形的三线合一.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
在半径为2a的⊙O中,弦AB长为2
a,则∠AOB为( )
| 3 |
| A、90° | B、120° |
| C、135° | D、150° |
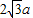 ,则∠AOB为( )
,则∠AOB为( )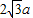 ,则∠AOB为( )
,则∠AOB为( )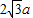 ,则∠AOB为( )
,则∠AOB为( ) ,则∠AOB为( )
,则∠AOB为( )