Question

【题目】如图，在平面直角坐标系中，直线分别交轴、轴于点和点，且，满足.

（1）______，______.

（2）点在直线的右侧，且：

①若点在轴上，则点的坐标为______；

②若为直角三角形，求点的坐标.

Answer 1

【答案】（1）－2，4；（2）①；②点的坐标为或.

【解析】

（1）利用非负数的的性质即可求出a，b；
（2）①利用等腰直角三角形的性质即可得出结论；
②分两种情况，利用等腰三角形的性质，及全等三角形的性质求出PC，BC，即可得出结论

解：（1）由题意，得，

所以且，

解得，；

（2）①如图，由（1）知，b=4，

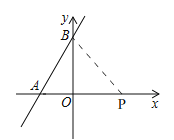
∴B（0，4），
∴OB=4，
点P在直线AB的右侧，且在x轴上，
∵∠APB=45°，
∴OP=OB=4，
∴点的坐标为.

②当时，过点作轴于点，

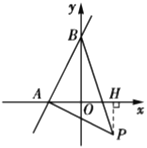
则，，

∴.

又∵，，

∴.

∴.

又∵，

∴.

∴，

.∴.

故点的坐标为.

当时，作轴，于点，

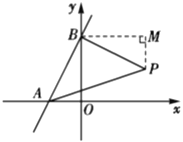
则， ，

∴ .

又∵，，

∴，

∴，

又∵ ，

∴.

，.

∴点的坐标为.

故点的坐标为或.