题目内容
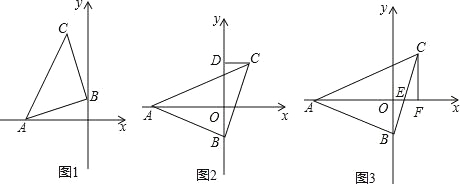
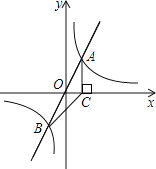
【题目】如图,在平面直角坐标系中,正比例函数y=3x与反比例函数y=![]() 的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.
的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.
(1)求反比例函数的表达式;
(2)求△ABC的面积;
(3)若点P是反比例函数y=![]() 图象上的一点,△OPC与△ABC面积相等,请直接写出点P的坐标.
图象上的一点,△OPC与△ABC面积相等,请直接写出点P的坐标.
【答案】(1)y=![]() ;(2)S△ABC=12;(3)P点坐标为(1,12)或(﹣1,﹣12).
;(2)S△ABC=12;(3)P点坐标为(1,12)或(﹣1,﹣12).
【解析】
(1)把A点横坐标代入正比例函数可求得A点坐标,代入反比例函数解析式可求得k,可求得反比例函数解析式;
(2)根据反比例函数的对称性得出点B的坐标,再利用三角形的面积公式解答即可;
(3)由条件可求得B、C的坐标,可先求得△ABC的面积,再结合△OPC与△ABC的面积相等求得P点坐标.
解:(1)把x=2代入y=3x中,得y=2×3=6,
∴点A坐标为(2,6),
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴k=2×6=12,
∴反比例函数的解析式为y=![]() ;
;
(2)∵AC⊥OC,
∴OC=2,
∵A、B关于原点对称,
∴B点坐标为(﹣2,﹣6),
∴B到OC的距离为6,
∴S△ABC=2S△ACO=2×![]() ×2×6=12,
×2×6=12,![]()
(3)∵S△ABC=12,
∴S△OPC=12,
设P点坐标为(x,![]() ),则P到OC的距离为|
),则P到OC的距离为|![]() |,
|,
∴![]() ×|
×|![]() |×2=12,解得x=1或﹣1,
|×2=12,解得x=1或﹣1,
∴P点坐标为(1,12)或(﹣1,﹣12).

【题目】(1)一个不透明的盒中装有若干个除颜色外都相同的红球与黄球.在这个口袋中先放入2个白球,再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色后放回盒中,再继续摸球,全班一共做了400次这样的摸球试验.如果知道摸出白球的频数是40,你能估计在未放入白球前,袋中原来共有多少个小球吗?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
球的类别 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
由上述的摸球试验推算:
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?