题目内容
已知:如图, 是⊙
是⊙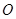 的直径
的直径 上任意一点,过点
上任意一点,过点 作
作 的垂线
的垂线 ,
, 是
是 的延长线上一点,联结
的延长线上一点,联结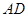 交⊙
交⊙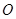 于点
于点 ,且
,且 .
.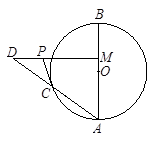
【小题1】判断直线
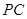 与⊙
与⊙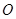 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;【小题2】若
 ,
,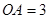 ,过点A作
,过点A作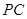 的平行线
的平行线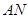 交⊙
交⊙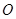 于点
于点 .求弦
.求弦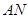 的长.
的长.
【小题1】联结CO, … …………………………………1分
∵DM⊥AB
∴∠D+∠A=90°
∵

∴∠D=∠PCD
∵OC=OA
∴∠A=∠OCA
∴∠OCA+∠PCD=90°
∴PC⊥OC
∴直线
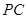 是⊙
是⊙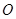 的切线
的切线【小题2】过点A作
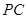 的平行线
的平行线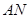 交⊙
交⊙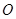 于点
于点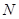 .
.∴∠NAC=∠PCD=∠D, AN⊥OC,设垂足是Q
∴Rt△
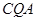 中
中∴
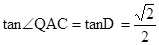
∴设CQ=x,AQ=
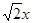
∴OQ=
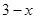
∵

∴
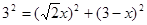
解得
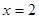 …………………………………4分
…………………………………4分∴
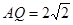
∴
 …………………………………5分解析:
…………………………………5分解析:(1)连接CO,然后求出∠OCA+∠PCD=90°,从而得出直线
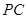 是⊙
是⊙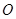 的切线;
的切线;(2)过点A作
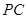 的平行线
的平行线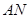 交⊙
交⊙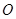 于点
于点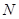 ,根据直角三角形勾股定理求出AQ的值,然后得出AN的值。
,根据直角三角形勾股定理求出AQ的值,然后得出AN的值。 
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
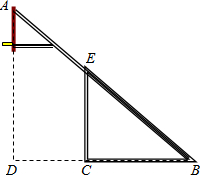 红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)
红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)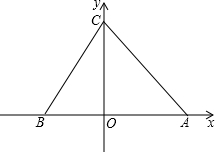 (2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
(2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
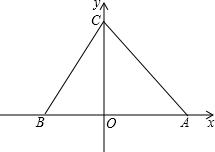 已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.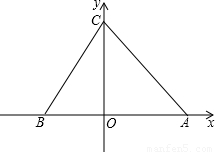 已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.