题目内容
坐标平面上,二次函数y= x2的图形过A、B两点,其中A、B两点的x坐标分别为2、4.若自A作y轴的平行线,自B作x轴的平行线,且两线交于C点,则C点坐标为( )
x2的图形过A、B两点,其中A、B两点的x坐标分别为2、4.若自A作y轴的平行线,自B作x轴的平行线,且两线交于C点,则C点坐标为( )A.(2,8)
B.(2,2
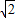 )
)C.(4,2)
D.(4,2
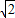 )
)
【答案】分析:自A作y轴的平行线,自B作x轴的平行线,且两线交于C点,则C点坐标的横坐标为A点的横坐标,纵坐标为B点纵坐标.
解答:解:自A作y轴的平行线,所以C点得横坐标x=2,
将B点横坐标代入解析式中,得纵坐标为8,
由已知得自B作x轴的平行线,所以C点纵坐标y=8,
C(2,8),
故选A.
点评:主要考查了二次函数图象上点的坐标特征,画出草图,容易解答.
解答:解:自A作y轴的平行线,所以C点得横坐标x=2,
将B点横坐标代入解析式中,得纵坐标为8,
由已知得自B作x轴的平行线,所以C点纵坐标y=8,
C(2,8),
故选A.
点评:主要考查了二次函数图象上点的坐标特征,画出草图,容易解答.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
坐标平面上,二次函数y=
x2的图形过A、B两点,其中A、B两点的x坐标分别为2、4.若自A作y轴的平行线,自B作x轴的平行线,且两线交于C点,则C点坐标为( )
| 1 |
| 2 |
| A、(2,8) | ||
B、(2,2
| ||
| C、(4,2) | ||
D、(4,2
|
 x2的图形过A、B两点,其中A、B两点的x坐标分别为2、4.若自A作y轴的平行线,自B作x轴的平行线,且两线交于C点,则C点坐标为( )
x2的图形过A、B两点,其中A、B两点的x坐标分别为2、4.若自A作y轴的平行线,自B作x轴的平行线,且两线交于C点,则C点坐标为( )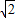 )
)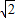 )
) x2的图形过A、B两点,其中A、B两点的x坐标分别为2、4.若自A作y轴的平行线,自B作x轴的平行线,且两线交于C点,则C点坐标为( )
x2的图形过A、B两点,其中A、B两点的x坐标分别为2、4.若自A作y轴的平行线,自B作x轴的平行线,且两线交于C点,则C点坐标为( )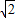 )
) )
)