题目内容
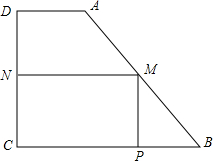 如图有一块形状是直角梯形的铁皮ABCD,它的上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现在要截成一个矩形铁皮MPCN,使它的顶点M、P、N分别在AB、BC、CD上,当MN多长时,矩形MPCN的面积有最大值,并请你求出这个最大值.
如图有一块形状是直角梯形的铁皮ABCD,它的上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现在要截成一个矩形铁皮MPCN,使它的顶点M、P、N分别在AB、BC、CD上,当MN多长时,矩形MPCN的面积有最大值,并请你求出这个最大值.
解: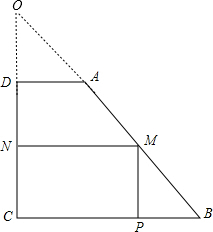
延长BA和CD交于O,
∵AD∥BC,
∴△ODA∽△OCB,
∴ =
= ,
,
∴ =
=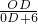 ,
,
OD= ,
,
∴OC=6+ =9.6,
=9.6,
∵四边形CNMP是矩形,
∴MN∥CP,
∴△ONM∽△OCB,
∴ =
= ,
,
∴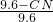 =
=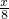 ,
,
∴CN=-1.2x+9.6,
∴矩形MPCN的面积S=x(-1.2x+9.6)=-1.2x2+9.6x=-1.2(x-4)2+19.2
当MN=4cm时,面积最大.最大面积为19.2cm2.
分析:延长BA和CD交于O,证△ODA∽△OCB,得出 =
= ,求出OD=
,求出OD= ,OC=9.6,证△ONM∽△OCB,求出CN=-1.2x+9.6,根据矩形MPCN的面积S=x(-1.2x+9.6)=-1.2(x-4)2+19.2,即可得出答案.
,OC=9.6,证△ONM∽△OCB,求出CN=-1.2x+9.6,根据矩形MPCN的面积S=x(-1.2x+9.6)=-1.2(x-4)2+19.2,即可得出答案.
点评:本题考查了二次函数的最值,矩形性质,相似三角形的性质和判定的应用,主要考查学生综合运用性质进行计算的能力.

延长BA和CD交于O,
∵AD∥BC,
∴△ODA∽△OCB,
∴
 =
= ,
,∴
 =
=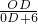 ,
,OD=
 ,
,∴OC=6+
 =9.6,
=9.6,∵四边形CNMP是矩形,
∴MN∥CP,
∴△ONM∽△OCB,
∴
 =
= ,
,∴
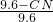 =
=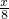 ,
,∴CN=-1.2x+9.6,
∴矩形MPCN的面积S=x(-1.2x+9.6)=-1.2x2+9.6x=-1.2(x-4)2+19.2
当MN=4cm时,面积最大.最大面积为19.2cm2.
分析:延长BA和CD交于O,证△ODA∽△OCB,得出
 =
= ,求出OD=
,求出OD= ,OC=9.6,证△ONM∽△OCB,求出CN=-1.2x+9.6,根据矩形MPCN的面积S=x(-1.2x+9.6)=-1.2(x-4)2+19.2,即可得出答案.
,OC=9.6,证△ONM∽△OCB,求出CN=-1.2x+9.6,根据矩形MPCN的面积S=x(-1.2x+9.6)=-1.2(x-4)2+19.2,即可得出答案.点评:本题考查了二次函数的最值,矩形性质,相似三角形的性质和判定的应用,主要考查学生综合运用性质进行计算的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
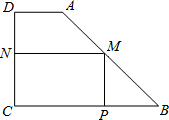 如图,有一块形状是直角梯形的铁皮ABCD,上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现要截成一矩形铁皮MPCN,使它的顶点M、P、N在AB、BC、CD上,设MN的长为x,矩形MPCN的面积为y.
如图,有一块形状是直角梯形的铁皮ABCD,上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现要截成一矩形铁皮MPCN,使它的顶点M、P、N在AB、BC、CD上,设MN的长为x,矩形MPCN的面积为y.
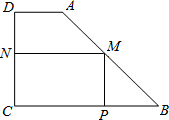 如图,有一块形状是直角梯形的铁皮ABCD,上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现要截成一矩形铁皮MPCN,使它的顶点M、P、N在AB、BC、CD上,设MN的长为x,矩形MPCN的面积为y.
如图,有一块形状是直角梯形的铁皮ABCD,上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现要截成一矩形铁皮MPCN,使它的顶点M、P、N在AB、BC、CD上,设MN的长为x,矩形MPCN的面积为y.