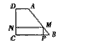题目内容
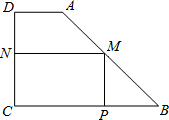 如图,有一块形状是直角梯形的铁皮ABCD,上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现要截成一矩形铁皮MPCN,使它的顶点M、P、N在AB、BC、CD上,设MN的长为x,矩形MPCN的面积为y.
如图,有一块形状是直角梯形的铁皮ABCD,上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现要截成一矩形铁皮MPCN,使它的顶点M、P、N在AB、BC、CD上,设MN的长为x,矩形MPCN的面积为y.(1)求y与x之间的关系式,并指出x的取值范围.
(2)当x为何值时,矩形MPCN的面积最大?最大面积是多少?
分析:(1)过A作BC的垂线,垂足是E,则△AEB∽△MPB,根据相似三角形的对应边的比相等,即可用x表示出PB的长,进而求得CP,则函数解析式即可求解;
(2)根据所有的函数解析式是二次函数,利用二次函数的性质即可求解.
(2)根据所有的函数解析式是二次函数,利用二次函数的性质即可求解.
解答: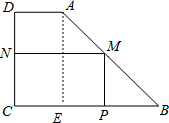 解:(1)过A作BC的垂线,垂足是E.
解:(1)过A作BC的垂线,垂足是E.
又∵MP⊥BC
∴AE∥MP
∴△AEB∽△MPB
∴
=
即
=
,解得:MP=
则y=x(
)=-
x2+
x (3<x≤6);
(2)∵y=-
x2+
x=-
(x2-8x+16-16)=-
(x-4)2+
,
∴当x=4时,有最大面积为:
.
 解:(1)过A作BC的垂线,垂足是E.
解:(1)过A作BC的垂线,垂足是E.又∵MP⊥BC
∴AE∥MP
∴△AEB∽△MPB
∴
| AE |
| MP |
| BE |
| PB |
即
| 6 |
| MP |
| 5 |
| 8-x |
| 48-6x |
| 5 |
则y=x(
| 48-6x |
| 5 |
| 6 |
| 5 |
| 48 |
| 5 |
(2)∵y=-
| 6 |
| 5 |
| 48 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 96 |
| 5 |
∴当x=4时,有最大面积为:
| 96 |
| 5 |
点评:本题考查的是相似三角形在实际生活中的应用,是二次函数与相似三角形相结合的题目,把求面积的最值的问题通过二次函数的性质转化为函数的最值问题.

练习册系列答案
相关题目

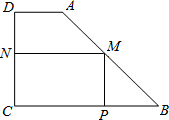 如图,有一块形状是直角梯形的铁皮ABCD,上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现要截成一矩形铁皮MPCN,使它的顶点M、P、N在AB、BC、CD上,设MN的长为x,矩形MPCN的面积为y.
如图,有一块形状是直角梯形的铁皮ABCD,上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现要截成一矩形铁皮MPCN,使它的顶点M、P、N在AB、BC、CD上,设MN的长为x,矩形MPCN的面积为y.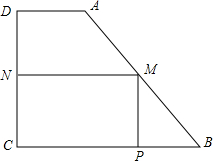 如图有一块形状是直角梯形的铁皮ABCD,它的上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现在要截成一个矩形铁皮MPCN,使它的顶点M、P、N分别在AB、BC、CD上,当MN多长时,矩形MPCN的面积有最大值,并请你求出这个最大值.
如图有一块形状是直角梯形的铁皮ABCD,它的上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现在要截成一个矩形铁皮MPCN,使它的顶点M、P、N分别在AB、BC、CD上,当MN多长时,矩形MPCN的面积有最大值,并请你求出这个最大值.