题目内容
 (2012•道里区三模)如图,正方形网格中的每个小正方形边长都为1,以每个小正方形顶点为顶点按下列要求在图1和图2中分别画三角形和平行四边形.
(2012•道里区三模)如图,正方形网格中的每个小正方形边长都为1,以每个小正方形顶点为顶点按下列要求在图1和图2中分别画三角形和平行四边形.(1)使三角形三边长为2、3、
| 13 |
(2)使平行四边形有一锐角为45°,且面积为4.
分析:(1)根据勾股定理逆定理,所作三角形是以
为斜边的直角三角形,利用网格结构作出两直角边分别为2、3的直角三角形即可;
(2)根据网格结构,作45°锐角,且使平行四边形的底边是2,高是2即可.
| 13 |
(2)根据网格结构,作45°锐角,且使平行四边形的底边是2,高是2即可.
解答:解:(1)∵22+32=13=
2,
∴所求作的三角形是以
为斜边的直角三角形,
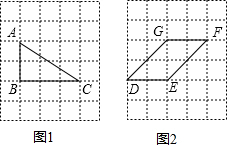
如图所示,△ABC即为所求作的三角形;
(2)如图所示,?DEFG即为所求作的平行四边形.
| 13 |
∴所求作的三角形是以
| 13 |
如图所示,△ABC即为所求作的三角形;
(2)如图所示,?DEFG即为所求作的平行四边形.

点评:本题考查了应用与设计作图,(1)根据勾股定理逆定理判断出所求作的三角形是直角三角形是解题的关键,解答此类题目熟练掌握并灵活运用网格结构非常重要.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
