题目内容
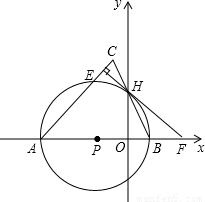
(2006•鄂尔多斯)如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于C,过点C的直线y=2x+b交x轴于D,且⊙P的半径为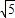 ,AB=4.
,AB=4.(1)求点B,P,C的坐标;
(2)求证:CD是⊙P的切线;
(3)若二次函数y=-x2+(a+1)x+6的图象经过点B,求这个二次函数的解析式,并写出使二次函数值小于一次函数y=2x+b值的x的取值范围.

【答案】分析:(1)连接CA,构造直角三角形,运用勾股定理,求出各线段的长,进而求出B,P,C的坐标;
(2)根据一次函数图象上点的坐标特征,求出对应线段的长,证明△DAC≌△POB,然后得到∠DCA=∠ABC,再根据直角三角形的性质求出∠DCA+∠ACB=90°,利用切线判定定理即可解答;
(3)把点B代入y=-x2+(a+1)x+6即可求出a的值,进而求出函数解析式;求出两函数图象交点,由图可得结论.
解答: (1)解:如图,连接CA.
(1)解:如图,连接CA.
∵OP⊥AB,
∴OB=OA=2.(1分)
∵OP2+BO2=BP2
∴OP2=5-4=1,OP=1.(2分)
∵BC是⊙P的直径,
∴∠CAB=90°.(也可用勾股定理求得下面的结论)
∵CP=BP,OB=OA,
∴AC=2OP=2.(3分)
∴B(2,0),P(0,1),C(-2,2).(写错一个不扣分)(4分)
(2)证明:∵y=2x+b过C点,
∴b=6∴y=2x+6.(5分)
∵当y=0时,x=-3,
∴D(-3,0).
∴AD=1.(6分)
∵OB=AC=2,AD=OP=1,∠CAD=∠POB=90°,
∴△DAC≌△POB.
∴∠DCA=∠ABC.
∵∠ACB+∠CBA=90°,
∴∠DCA+∠ACB=90°.(也可用勾股定理逆定理证明)(7分)
∴DC是⊙P的切线.(8分)
(3)解:∵y=-x2+(a+1)x+6过B(2,0)点,
∴0=-22+(a+1)×2+6.
∴a=-2.(9分)
∴y=-x2-x+6.(10分)
因为函数y=-x2-x+6与y=2x+6的图象交点是(0,6)和点D(-3,0)(画图可得此结论)(11分)
所以满足条件的x的取值范围是x<-3或x>0.(12分)
点评:本题是一道较为常规的综合压轴题,综合性较强,解第3小题时可以借助函数图象来很明了快捷地得出结论.
(2)根据一次函数图象上点的坐标特征,求出对应线段的长,证明△DAC≌△POB,然后得到∠DCA=∠ABC,再根据直角三角形的性质求出∠DCA+∠ACB=90°,利用切线判定定理即可解答;
(3)把点B代入y=-x2+(a+1)x+6即可求出a的值,进而求出函数解析式;求出两函数图象交点,由图可得结论.
解答:
 (1)解:如图,连接CA.
(1)解:如图,连接CA.∵OP⊥AB,
∴OB=OA=2.(1分)
∵OP2+BO2=BP2
∴OP2=5-4=1,OP=1.(2分)
∵BC是⊙P的直径,
∴∠CAB=90°.(也可用勾股定理求得下面的结论)
∵CP=BP,OB=OA,
∴AC=2OP=2.(3分)
∴B(2,0),P(0,1),C(-2,2).(写错一个不扣分)(4分)
(2)证明:∵y=2x+b过C点,
∴b=6∴y=2x+6.(5分)
∵当y=0时,x=-3,
∴D(-3,0).
∴AD=1.(6分)
∵OB=AC=2,AD=OP=1,∠CAD=∠POB=90°,
∴△DAC≌△POB.
∴∠DCA=∠ABC.
∵∠ACB+∠CBA=90°,
∴∠DCA+∠ACB=90°.(也可用勾股定理逆定理证明)(7分)
∴DC是⊙P的切线.(8分)
(3)解:∵y=-x2+(a+1)x+6过B(2,0)点,
∴0=-22+(a+1)×2+6.
∴a=-2.(9分)
∴y=-x2-x+6.(10分)
因为函数y=-x2-x+6与y=2x+6的图象交点是(0,6)和点D(-3,0)(画图可得此结论)(11分)
所以满足条件的x的取值范围是x<-3或x>0.(12分)
点评:本题是一道较为常规的综合压轴题,综合性较强,解第3小题时可以借助函数图象来很明了快捷地得出结论.

练习册系列答案
相关题目
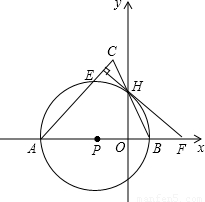
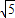 ,AB=4.
,AB=4.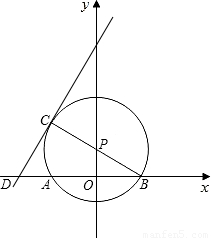
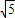 ,AB=4.
,AB=4.