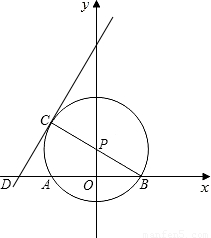
题目内容
(2006•鄂尔多斯)如图,在△ABC中,AB=AC=5,以AB为直径的⊙P交BC于H.点A,B在x轴上,点H在y轴上,B点的坐标为(1,0).(1)求点A,H,C的坐标;
(2)过H点作AC的垂线交AC于E,交x轴于F,求证:EF是⊙P的切线;
(3)求经过A,O两点且顶点到x轴的距离等于4的抛物线解析式.
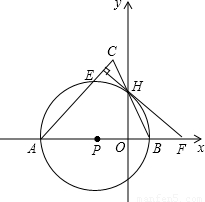
【答案】分析:(1)连接AH,根据AB是⊙P的直径,先证明△HOB∽△AOH,得OH2=OA•OB,OH=2,过C点作CM⊥y轴于M,所以CH=HB,可证明△CHM≌△BHO,所以CM=OB,MH=OH,OM=4,CM=1,即A(-4,0),H(0,2),C(-1,4).
(2)连接HP,CH=BH,AP=PB证得HP∥AC,根据EF⊥AC,可知PH⊥EF,所以EF是⊙P的切线.
(3)设抛物线方程为y=a1(x+2)2+4或y=a2(x+2)2-4,由抛物线的顶点坐标为(-2,4)或(-2,-4)可知,分别代入x=0,y=0得:a1=-1,a2=1,可求抛物线的解析式为y=-(x+2)2+4或y=(x+2)2-4.
解答: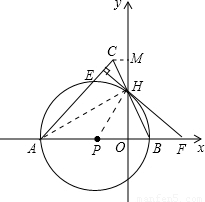 解:如图
解:如图
(1)连接AH,
∵AB是⊙P的直径,
∴∠AHB=90°(1分)
∵∠HOB=90°,∠OHB=∠HAO,
∴△HOB∽△AOH
∴OH2=OA•OB,
∴OH2=4×1
∴OH=2(2分)
过C点作CM⊥y轴于M,
∵AB=AC,∠AHB=90°
∴CH=HB(3分)
∵∠CHM=∠OHB,△CHM≌△BHO
∴CM=OB,MH=OH,
∴OM=4,CM=1,(4分)
∴A(-4,0),H(0,2),C(-1,4)(写错一个不扣分)(5分)
(或过C点作CM⊥x轴于M,用中位线定理求得OM=1,CM=4).
(2)证法一:连接HP,
∵CH=BH,AP=PB,
∴HP∥AC,(6分)
∵EF⊥AC,
∴PH⊥EF,(7分)
∴EF是⊙P的切线.(8分)
证法二:
∵AB=AC,
∴∠ACH=∠ABH,
∵HP=PB,
∴∠PHB=∠PBH
∴∠PHB=∠ACH(6分)
∵∠ACH+∠EHC=90°,∠EHC=∠BHF
∴∠PHB+∠BHF=90°(7分)
∴EF是⊙P的切线.(8分)
(3)解法一:
由题意知:抛物线的顶点坐标为(-2,4)或(-2,-4),(9分)
设抛物线方程为y=a1(x+2)2+4或y=a2(x+2)2-4(10分),
分别代入x=0,y=0得:a1=-1,a2=1,(11分)
∴抛物线的解析式为y=-(x+2)2+4或y=(x+2)2-4.(12分)
解法二:(简要过程)
设抛物线的方程为y=ax2+bx+c,代入顶点坐标(-2,4)或(-2,-4)(9分)
以及(0,0),(-4,0)得两个三元一次方程组,(10分)
解方程组得c1=0,a1=-1,b1=-4;c2=0,a2=1,b2=4;(11分)
∴抛物线的解析式为y=x2+4x或y=-x2-4x.(12分)
点评:本题考查二次函数的综合应用,其中涉及到的知识点有待定系数法求函数解析式,交点的意义和圆中的有关性质等.要熟练掌握才能灵活运用.
(2)连接HP,CH=BH,AP=PB证得HP∥AC,根据EF⊥AC,可知PH⊥EF,所以EF是⊙P的切线.
(3)设抛物线方程为y=a1(x+2)2+4或y=a2(x+2)2-4,由抛物线的顶点坐标为(-2,4)或(-2,-4)可知,分别代入x=0,y=0得:a1=-1,a2=1,可求抛物线的解析式为y=-(x+2)2+4或y=(x+2)2-4.
解答:
 解:如图
解:如图(1)连接AH,
∵AB是⊙P的直径,
∴∠AHB=90°(1分)
∵∠HOB=90°,∠OHB=∠HAO,
∴△HOB∽△AOH
∴OH2=OA•OB,
∴OH2=4×1
∴OH=2(2分)
过C点作CM⊥y轴于M,
∵AB=AC,∠AHB=90°
∴CH=HB(3分)
∵∠CHM=∠OHB,△CHM≌△BHO
∴CM=OB,MH=OH,
∴OM=4,CM=1,(4分)
∴A(-4,0),H(0,2),C(-1,4)(写错一个不扣分)(5分)
(或过C点作CM⊥x轴于M,用中位线定理求得OM=1,CM=4).
(2)证法一:连接HP,
∵CH=BH,AP=PB,
∴HP∥AC,(6分)
∵EF⊥AC,
∴PH⊥EF,(7分)
∴EF是⊙P的切线.(8分)
证法二:
∵AB=AC,
∴∠ACH=∠ABH,
∵HP=PB,
∴∠PHB=∠PBH
∴∠PHB=∠ACH(6分)
∵∠ACH+∠EHC=90°,∠EHC=∠BHF
∴∠PHB+∠BHF=90°(7分)
∴EF是⊙P的切线.(8分)
(3)解法一:
由题意知:抛物线的顶点坐标为(-2,4)或(-2,-4),(9分)
设抛物线方程为y=a1(x+2)2+4或y=a2(x+2)2-4(10分),
分别代入x=0,y=0得:a1=-1,a2=1,(11分)
∴抛物线的解析式为y=-(x+2)2+4或y=(x+2)2-4.(12分)
解法二:(简要过程)
设抛物线的方程为y=ax2+bx+c,代入顶点坐标(-2,4)或(-2,-4)(9分)
以及(0,0),(-4,0)得两个三元一次方程组,(10分)
解方程组得c1=0,a1=-1,b1=-4;c2=0,a2=1,b2=4;(11分)
∴抛物线的解析式为y=x2+4x或y=-x2-4x.(12分)
点评:本题考查二次函数的综合应用,其中涉及到的知识点有待定系数法求函数解析式,交点的意义和圆中的有关性质等.要熟练掌握才能灵活运用.

练习册系列答案
相关题目
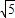 ,AB=4.
,AB=4.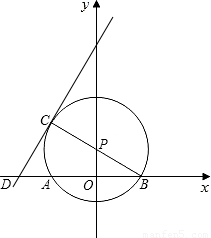
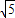 ,AB=4.
,AB=4.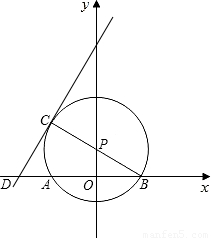
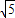 ,AB=4.
,AB=4.