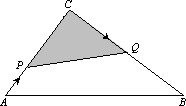
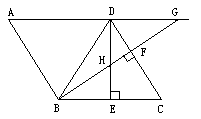
题目内容
| |||||||||||||||||||
答案:
解析:
解析:
(1) |
S△PCQ= 解得 ∴当时间 |
(2) |
当0< 当2< |
(3) |
①当0< ②当2< ③当3< |
(4) |
①在0< ②在2< ③在3< ∵S1<S2<S3 ∴ |

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目