题目内容
【题目】已知：如图，E、F是平行四边行ABCD的对角线AC上的 两点，AE=CF。
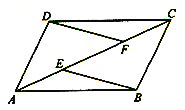
求证：（1）△ADF≌△CBE
（2）EB∥DF．
【答案】∵四边形ABCD为平行四边形，
∴AD∥BC，AD＝BC. ………………(1分)
∴∠DAC＝∠BCE.
又∵AE＝CF，∴AF＝CE
∴△ADF≌△CBE.……………………(4分)
∴∠AFD＝∠CEB.
∴BE∥DF. ……………………………(6分
【解析】试题分析：要证△ADF≌△CBE，因为AE=CF，则两边同时加上EF，得到AF=CE，又因为ABCD是平行四边形，得出AD=CB，∠DAF=∠BCE，从而根据SAS推出两三角形全等，由全等可得到∠DFA=∠BEC，所以得到DF∥EB．
证明：（1）∵AE=CF，
∴AE+EF=CF+FE，即AF=CE．
又ABCD是平行四边形，
∴AD=CB，AD∥BC．
∴∠DAF=∠BCE．
在△ADF与△CBE中
，
∴△ADF≌△CBE（SAS）．
（2）∵△ADF≌△CBE，
∴∠DFA=∠BEC．
∴DF∥EB．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
【题目】小红随机调查了50名九年级同学某次知识问卷的得分情况，结果如下表：
问卷得分（单位：分） | 65 | 70 | 75 | 80 | 85 |
人数（单位：人） | 1 | 15 | 15 | 16 | 3 |
则这50名同学问卷得分的众数和中位数分别是 （ ）
A. 16，75 B. 80，75 C. 75，80 D. 16，15