题目内容
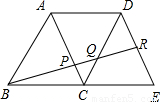
如图,⊙O和⊙O′都经过点A、B,点P在BA延长线上,过P作⊙O的割线PCD交⊙O于C、D两点,作⊙O′的切线PE切⊙O′于点E.若PC=4,CD=8,⊙O的半径为5.(1)求PE的长;
(2)求△COD的面积.

【答案】分析:(1)在⊙O中,根据割线定理,得PC•PD=PA•PB;在⊙O′中,由切割线定理,得PE2=PA•PB;联立两式得PE2=PC•PD,由此可求出PE的长.
(2)△COD中,已知底边CD的长,需求出CD边上的高;过O作CD的垂线,设垂足为F;由垂径定理得CF=FD=4;在Rt△COF中,已知了OC的长,可用勾股定理求出OF的长;进而可根据三角形的面积公式求得△COD的面积.
解答: 解:(1)∵PD、PB分别交⊙O于C、D和A、B;
解:(1)∵PD、PB分别交⊙O于C、D和A、B;
根据割线定理得PA•PB=PC•PD.
又∵PE为⊙O′的切线,PAB为⊙O′的割线;
根据切割线定理得PE2=PA•PB.
即PE2=PC•PD=4×(4+8)=48;
∴PE=4 .
.
(2)在⊙O中过O点作OF⊥CD,垂足为F;
根据垂径定理知OF平分弦CD,即CF= CD=4;
CD=4;
在Rt△OFC中,OF2=OC2-CF2=52-42=9;
∴OF=3;
∴S△COD= CD•OF=
CD•OF= ×8×3=12个面积单位.
×8×3=12个面积单位.
点评:本题考查了切割线定理、垂径定理、勾股定理等知识.求圆的弦长、弦心距的问题可以转化为解直角三角形的问题.
(2)△COD中,已知底边CD的长,需求出CD边上的高;过O作CD的垂线,设垂足为F;由垂径定理得CF=FD=4;在Rt△COF中,已知了OC的长,可用勾股定理求出OF的长;进而可根据三角形的面积公式求得△COD的面积.
解答:
 解:(1)∵PD、PB分别交⊙O于C、D和A、B;
解:(1)∵PD、PB分别交⊙O于C、D和A、B;根据割线定理得PA•PB=PC•PD.
又∵PE为⊙O′的切线,PAB为⊙O′的割线;
根据切割线定理得PE2=PA•PB.
即PE2=PC•PD=4×(4+8)=48;
∴PE=4
 .
.(2)在⊙O中过O点作OF⊥CD,垂足为F;
根据垂径定理知OF平分弦CD,即CF=
 CD=4;
CD=4;在Rt△OFC中,OF2=OC2-CF2=52-42=9;
∴OF=3;
∴S△COD=
 CD•OF=
CD•OF= ×8×3=12个面积单位.
×8×3=12个面积单位.点评:本题考查了切割线定理、垂径定理、勾股定理等知识.求圆的弦长、弦心距的问题可以转化为解直角三角形的问题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
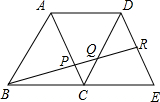 如图四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.则图中相似三角形(相似比为1 除外)有( )
如图四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.则图中相似三角形(相似比为1 除外)有( )