题目内容
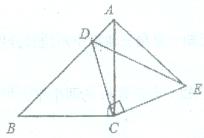
如图∆ABC和∆ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,试说明:(1)∆ACE≌∆BCD;(2)AD2+DB2=DE2。
解:(1)∠ACB=∠DCE=90°
∴∠BCD=∠ACE
又BC=AC,DC=EC
∴△BCD≌△ACE(SAS)
(2)∵△BCD≌△ACE
∴BD=AE
∠B=∠CAE
又∠B+∠BAC=90°
∴∠EAD=∠EAC+∠CAB=90°
在Rt△ADE中,由勾股定理
![]()
即![]()

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目



