题目内容
已知⊙O的半径OA=2,弦AB、AC的长分别是2| 2 |
| 3 |
分析:根据两条弦的长分别求出两条弦所对的圆心角的度数和两条弦的弦心距,然后求出两条弦所对的弓形的面积,进而分两种情况分别求出两弦所成的角所夹的圆内部分的面积.
解答:解:如图:作OD⊥AC于D,OE⊥AB于E,连接OA,
∵AB=2
,AC=2
,
∴AD=
,AE=
,
∵OA=2,
∴OD=1,OE=
,
∴∠DOA=60°,∠AOE=45°,
∴∠COA=120°,∠AOB=90°,
∴S弓形AC=S扇形OAC-S△OAC=
-
=
π-
,
S弓形AB=S扇形OAB-S△OAB=
-
=π-2,
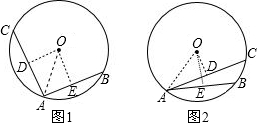
∴①当两条弦在圆心的异侧时,如图1,
∠CAB所夹的圆内部分的面积=S圆O-S弓形AC-S弓形AB=π×22-(
π-
)-(π-2)=
+2+
;
②当两条弦在圆心的同侧时,如图2,
∠CAB所夹的圆内部分的面积=S弓形AC-S弓形AB=(
π-
)-(π-2)=
+2-
.
故答案为:
+2+
或
+2-
.
∵AB=2
| 3 |
| 2 |
∴AD=
| 3 |
| 2 |
∵OA=2,
∴OD=1,OE=
| 2 |
∴∠DOA=60°,∠AOE=45°,
∴∠COA=120°,∠AOB=90°,
∴S弓形AC=S扇形OAC-S△OAC=
| 120π×22 |
| 360 |
2
| ||
| 2 |
| 4 |
| 3 |
| 3 |
S弓形AB=S扇形OAB-S△OAB=
| 90π×22 |
| 360 |
2
| ||||
| 2 |

∴①当两条弦在圆心的异侧时,如图1,
∠CAB所夹的圆内部分的面积=S圆O-S弓形AC-S弓形AB=π×22-(
| 4 |
| 3 |
| 3 |
| 5π |
| 3 |
| 3 |
②当两条弦在圆心的同侧时,如图2,
∠CAB所夹的圆内部分的面积=S弓形AC-S弓形AB=(
| 4 |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
故答案为:
| 5π |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
点评:本题考查了扇形及弓形面积的计算、垂径定理及勾股定理的知识,正确的解题的关键是分两种情况讨论.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知⊙O的半径OA=10cm,弦AB=16cm,P为弦AB上的一个动点,则OP的最短距离为( )
| A、5cm | B、6cm | C、8cm | D、10cm |
 如图,已知⊙O的半径OA=
如图,已知⊙O的半径OA= 如图,已知⊙O的半径OA=6,B为⊙O上一点,∠ABC=45°,则∠AOC所对的弧AC的长为
如图,已知⊙O的半径OA=6,B为⊙O上一点,∠ABC=45°,则∠AOC所对的弧AC的长为 (2013•来宾)如图是一圆形水管的截面图,已知⊙O的半径OA=13,水面宽AB=24,则水的深度CD是
(2013•来宾)如图是一圆形水管的截面图,已知⊙O的半径OA=13,水面宽AB=24,则水的深度CD是