Question

已知⊙O的半径OA=10cm，弦AB=16cm，P为弦AB上的一个动点，则OP的最短距离为（　　）

• A、5cm
• B、6cm
• C、8cm
• D、10cm

Answer 1

分析：根据直线外一点到直线上任一点的线段长中垂线段最短得到当OP为垂线段时，即OP⊥AB，OP的最短，再根据垂径定理得到AP=BP=

1

2

AB=

1

2

×16=8，然后根据勾股定理计算出OP即可．

解答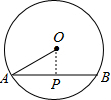：解：当OP为垂线段时，即OP⊥AB，OP的最短，如图，
∴AP=BP=

1

2

AB=

1

2

×16=8，
而OA=10，
在Rt△OAP中，
OP=

OA2-AP2

=

102-82

=6（cm）．
故选B．

点评：本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧；也考查了垂线段最短以及勾股定理．