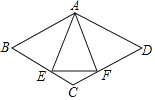
题目内容
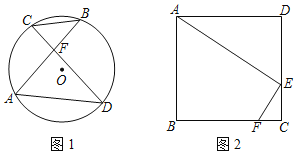
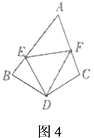
【题目】问题背景:如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 是正方形,求图中阴影部分的面积.
是正方形,求图中阴影部分的面积.
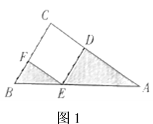
(1)发现:如图![]() ,小芳发现,只要将
,小芳发现,只要将![]() 绕点
绕点![]() 逆时针旋转一定的角度到达
逆时针旋转一定的角度到达![]() ,就能将阴影部分转化到一个三角形里,从而轻松解答.根据小芳的发现,可求出图1中阴影部分的面积为______;(直接写出答案)
,就能将阴影部分转化到一个三角形里,从而轻松解答.根据小芳的发现,可求出图1中阴影部分的面积为______;(直接写出答案)
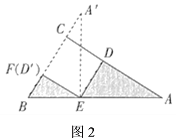
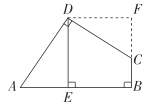
(2)应用:如图![]() ,在四边形
,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 的长;
的长;
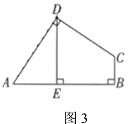
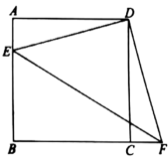
(3)拓展:如图![]() ,在四边形
,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点作
为顶点作![]() 为
为![]() 角,角的两边分别交
角,角的两边分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,连接
两点,连接![]() ,请直接写出线段
,请直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【答案】(1)30;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意根据全等三角形的性质以及运用等量代换得出![]() ,进而得出
,进而得出![]() 的面积即阴影部分的面积;
的面积即阴影部分的面积;
(2)由题意把![]() 绕点
绕点![]() 旋转到
旋转到![]() 处,使
处,使![]() 与
与![]() 重合,利用全等三角形的性质进行等量代换得出
重合,利用全等三角形的性质进行等量代换得出![]() ,进而进行分析即可;
,进而进行分析即可;
(3)根据题意延长AC到G,使CG=BE,并构造全等三角形,运用全等三角形的判定和性质进行分析即可 .
解:(1)∵![]() 绕点
绕点![]() 逆时针旋转一定的角度到达
逆时针旋转一定的角度到达![]() ,
,
∴![]() ,
,
∵四边形![]() 是正方形,
是正方形,![]() ,
,
∴等量代换可知![]() ,
,
∵![]() ,
,![]() ,
,
∴阴影部分的面积即![]() 的面积为:
的面积为:![]() .
.
(2)如图,把![]() 绕点
绕点![]() 旋转到
旋转到![]() 处,使
处,使![]() 与
与![]() 重合,可得
重合,可得![]() .
.
![]() ,
,
![]() ,
,
即![]() ,
,![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
又![]() ,四个角都为
,四个角都为![]() ,
,
![]() 四边形
四边形![]() 是正方形,易得
是正方形,易得![]() .
.
![]() ,即
,即![]() .
.
(3)线段BE、CF、EF之间的数量关系为:EF=BE+CF.
理由:如图,延长AC到G,使CG=BE,

∵∠B+∠ACD=180°,∠ACD+∠DCG=180°,
∴∠B=∠DCG,
在△DBE和△DCG中,
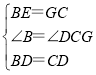 ,
,
∴△DBE≌△DCG(SAS),
∴DE=DG,∠BDE=∠CDG,
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°,
∴∠CDG+∠CDF=60°,
∴∠EDF=∠GDF,
在△EDF和△GDF中,
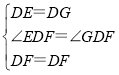 ,
,
∴△EDF≌△GDF(SAS),
∴EF=GF,
∵GF=CG+CF,
∴GF=BE+CF,
∴EF=BE+CF.