题目内容
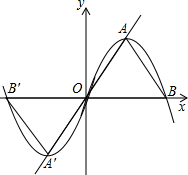 已知:抛物线y=ax2+bx与x铀的一个交点为B,顶点A在直线y=
已知:抛物线y=ax2+bx与x铀的一个交点为B,顶点A在直线y=| 3 |
(1)证明:△OAB为等边三角形;
(2)若△OAB的内切圆半径为1,求出抛物线的解析式;
(3)在抛物线上是否存在点P,使△POB是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
分析:(1)根据直线OA的斜率不难得到∠AOB=60°,根据抛物线的对称性可知AB=OA,由此得证.
(2)由于抛物线的开口方向不确定,因此分a>0和a<0两种情况求解.以a<0为例说明:
可设三角形AOB的内心为I,过A作AC⊥OB,则I必在AC上,连接IO,在构建的直角三角形IOC中,∠IOC=30°,已知了IC=1,即可求出OC和IO的长,也就能求出B点和A点的坐标,然后将这两点坐标代入抛物线中即可求出二次函数的解析式.(a>0时,解法完全相同).
(3)如果△POB是直角三角形,那么如果过P作x轴的垂线,根据射影定理即可得出P点纵坐标绝对值的平方等于P点横坐标绝对值和P、B两点横坐标差的绝对值的乘积.然后联立抛物线的解析式即可求出P点坐标.
(2)由于抛物线的开口方向不确定,因此分a>0和a<0两种情况求解.以a<0为例说明:
可设三角形AOB的内心为I,过A作AC⊥OB,则I必在AC上,连接IO,在构建的直角三角形IOC中,∠IOC=30°,已知了IC=1,即可求出OC和IO的长,也就能求出B点和A点的坐标,然后将这两点坐标代入抛物线中即可求出二次函数的解析式.(a>0时,解法完全相同).
(3)如果△POB是直角三角形,那么如果过P作x轴的垂线,根据射影定理即可得出P点纵坐标绝对值的平方等于P点横坐标绝对值和P、B两点横坐标差的绝对值的乘积.然后联立抛物线的解析式即可求出P点坐标.
解答: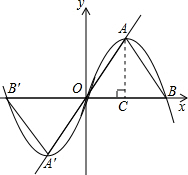 (1)证明:作AC⊥OB于点C;
(1)证明:作AC⊥OB于点C;
∵点A在直线y=
x上,设A(x,
x).
在直角三角形OAC中,tan∠AOC=
=
=
,
∴∠AOC=60°
由抛物线的对称性可知:OA=AB,
∴△AOB为等边三角形.
(2)解:当a<0时,设△AOB的内心为I,则∠IOC=30°,在直角三角形IOC中,
∵IC=1,OC=
.
∴抛物线的对称轴x=-
=
,
∴a=-1,b=2
.
∴抛物线的解析式为y=-x2+2
x.
当a>0时,同法可求,另一条抛物线的解析式为y=x2+2
x.
(3)解:易知:抛物线与x轴的两交点为O(0,0),B(-
,0).
且顶点A(-
,-
)在直线y=
x上,
∴-
=
(-
),
解得b=2
,b=0(舍去).
∴B(-
,0)
抛物线的解析式为y=ax2+2
x.
假设存在符合条件的点P(m,n).
过点P做PD⊥OB于D,则根据射影定理有: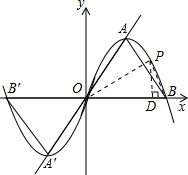
PD2=OD•BD;
由题意知:y=ax2+2
x,
∴
,
解得:
,
,
∴存在符合条件的P点,且坐标为:P(
,-
)或(
,-
).
 (1)证明:作AC⊥OB于点C;
(1)证明:作AC⊥OB于点C;∵点A在直线y=
| 3 |
| 3 |
在直角三角形OAC中,tan∠AOC=
| AC |
| OC |
| ||
| |x| |
| 3 |
∴∠AOC=60°
由抛物线的对称性可知:OA=AB,
∴△AOB为等边三角形.
(2)解:当a<0时,设△AOB的内心为I,则∠IOC=30°,在直角三角形IOC中,
∵IC=1,OC=
| 3 |
∴抛物线的对称轴x=-
| b |
| 2a |
| 3 |
∴a=-1,b=2
| 3 |
∴抛物线的解析式为y=-x2+2
| 3 |
当a>0时,同法可求,另一条抛物线的解析式为y=x2+2
| 3 |
(3)解:易知:抛物线与x轴的两交点为O(0,0),B(-
| b |
| a |
且顶点A(-
| b |
| 2a |
| b2 |
| 4a |
| 3 |
∴-
| b2 |
| 4a |
| 3 |
| b |
| 2a |
解得b=2
| 3 |
∴B(-
2
| ||
| a |
抛物线的解析式为y=ax2+2
| 3 |
假设存在符合条件的点P(m,n).
过点P做PD⊥OB于D,则根据射影定理有:

PD2=OD•BD;
由题意知:y=ax2+2
| 3 |
∴
|
解得:
|
|
∴存在符合条件的P点,且坐标为:P(
-
| ||||
| a |
| 1 |
| a |
-
| ||||
| a |
| 1 |
| a |
点评:本题是二次函数综合题,考查了等边三角形的判定、二次函数解析式的确定、三角形内心等知识点.综合性强,难度较大.

练习册系列答案
相关题目
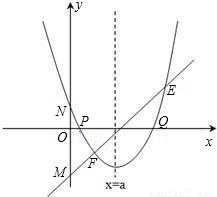
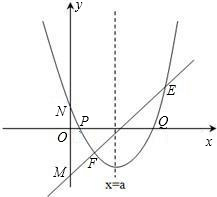 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.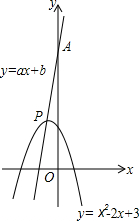 (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.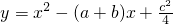 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否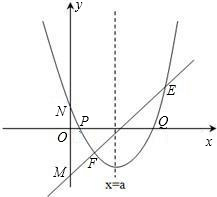 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.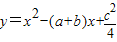 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.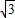 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.