题目内容
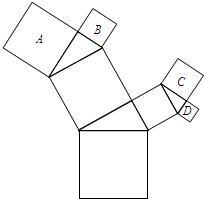 15、如图,所有的四边形都是正方形,所有三角形都是直角三角形,其中最大的正方形的边长是a,则图中四个小正方形A、B、C、D的面积之和是
15、如图,所有的四边形都是正方形,所有三角形都是直角三角形,其中最大的正方形的边长是a,则图中四个小正方形A、B、C、D的面积之和是a2
.分析:根据勾股定理知,以两条直角边为边作出的两个正方形面积和等于以斜边为边的正方形面积.
解答: 解:如图,由勾股定理可知,正方形A与B的面积和等于正方形M的面积.
解:如图,由勾股定理可知,正方形A与B的面积和等于正方形M的面积.
正方形C与D的面积和等于正方形N的面积.
并且正方形M与N的面积和等于最大的正方形的面积.因此A、B、C、D的面积之和是为最大正方形的面积=a2.
 解:如图,由勾股定理可知,正方形A与B的面积和等于正方形M的面积.
解:如图,由勾股定理可知,正方形A与B的面积和等于正方形M的面积.正方形C与D的面积和等于正方形N的面积.
并且正方形M与N的面积和等于最大的正方形的面积.因此A、B、C、D的面积之和是为最大正方形的面积=a2.
点评:本题考查了勾股定理的意义及应用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
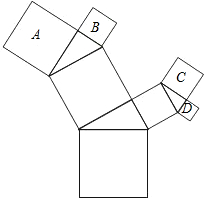 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm,B的边长为5cm,C的边长为5cm,则正方形D的边长为( )
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm,B的边长为5cm,C的边长为5cm,则正方形D的边长为( )A、
| ||
| B、4cm | ||
C、
| ||
| D、3cm |
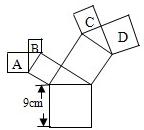 11、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为9cm,则正方形A,B,C,D的面积之和为( )
11、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为9cm,则正方形A,B,C,D的面积之和为( )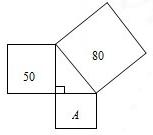 11、如图,所有的四边形都是正方形,已知其中两个正方形的面积分别为50和80,那么图中A的面积为
11、如图,所有的四边形都是正方形,已知其中两个正方形的面积分别为50和80,那么图中A的面积为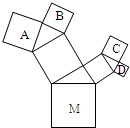 12、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中正方形A,B,C,D的面积之和为100cm2,则最大的正方形M的边长为
12、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中正方形A,B,C,D的面积之和为100cm2,则最大的正方形M的边长为