题目内容
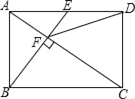
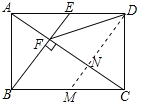
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() ;⑤S四边形CDEF=
;⑤S四边形CDEF=![]() S△ABF,其中正确的结论有( )
S△ABF,其中正确的结论有( )
A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
【解析】试题分析:过D作DM∥BE交AC于N,∵四边形ABCD是矩形,∴AD∥BC,∠ABC=90°,AD=BC,∵BE⊥AC于点F,∴∠EAC=∠ACB,∠ABC=∠AFE=90°,∴△AEF∽△CAB,故①正确;
∵AD∥BC,∴△AEF∽△CBF,∴![]() ,∵AE=
,∵AE=![]() AD=
AD=![]() BC,∴
BC,∴![]() ,∴CF=2AF,故②正确,
,∴CF=2AF,故②正确,
∵DE∥BM,BE∥DM,∴四边形BMDE是平行四边形,∴BM=DE=![]() BC,∴BM=CM,∴CN=NF,∵BE⊥AC于点F,DM∥BE,∴DN⊥CF,∴DF=DC,故③正确;
BC,∴BM=CM,∴CN=NF,∵BE⊥AC于点F,DM∥BE,∴DN⊥CF,∴DF=DC,故③正确;
∵tan∠CAD=![]() ,而CD与AD的大小不知道,∴tan∠CAD的值无法判断,故④错误;
,而CD与AD的大小不知道,∴tan∠CAD的值无法判断,故④错误;
∵△AEF∽△CBF,∴![]() ,∴S△AEF=
,∴S△AEF=![]() S△ABF,S△ABF=
S△ABF,S△ABF=![]() S矩形ABCD,∵S△ABE=
S矩形ABCD,∵S△ABE=![]() S矩形ABCD,S△ACD=
S矩形ABCD,S△ACD=![]() S矩形ABCD,∴S△AEF=
S矩形ABCD,∴S△AEF=![]() S四边形ABCD,又∵S四边形CDEF=S△ACD﹣S△AEF=
S四边形ABCD,又∵S四边形CDEF=S△ACD﹣S△AEF=![]() S矩形ABCD﹣
S矩形ABCD﹣![]() S矩形ABCD=
S矩形ABCD=![]() S矩形ABCD,∴S四边形CDEF=
S矩形ABCD,∴S四边形CDEF=![]() S△ABF,故⑤正确;
S△ABF,故⑤正确;
故选B.

【题目】2018年俄罗斯世界杯组委会对世界杯比赛用球进行抽查,随机抽取了100个足球,检测每个足球的质量是否符合标准,超过或不足部分分别用正、负数来表示,记录如表:
与标准质量的差值(单位:克) | ﹣4 | ﹣2 | 0 | 1 | 3 | 6 |
个数 | 10 | 13 | 30 | 25 | 15 | 7 |
(1)平均每个足球的质量比标准质量多还是少?用你学过的方法合理解释;
(2)若每个足球标准质量为420克,则抽样检测的足球的总质量是多少克?
【题目】某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信,这五封信的重量分别是![]() .根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:
.根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:
业务种类 | 计费单位 | 资费标准/元 | 挂号费/(元/封) | 特制信封(元/个) |
挂号信 | 首重100g,每重20g | 0.8 | 3 | 0.5 |
续重101~2000g,每重100g | 2.00 | |||
特制信封 | 首重1000g内 | 5.00 | 3 | 1.0 |
(1)重量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?
(2)这五封信分别以怎样的方式寄出最合算?请说明理由.
(3)通过解答上述问题,你有何启示?(请你用一两句话说明)