题目内容
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() 于
于![]() ,
,![]() 交于点
交于点![]() .
.
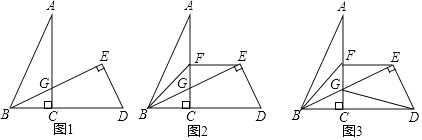
(1)如图1,请写出![]() 与
与![]() 的数量关系;
的数量关系;
(2)如图2,若![]() 平分
平分![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,如图3,连接![]() ,若
,若![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1) ![]() ;(2) 见解析;(3)
;(2) 见解析;(3) ![]() .
.
【解析】
(1)根据三角形的内角和定理可得∠DBE=180°-∠E-∠BDE=90°-∠BDE,∠A=180°-∠ACB-∠ABC=90°-∠ABC,再结合已知条件即可证出结论;
(2)根据角平分线的定义和三角形的内角和定理证出∠A=∠FEB,再结合(1)的结论可证∠FEB=∠DBE,根据平行线的判定证出EF∥BD,从而证出∠EFC=∠ACB=90°,再根据垂直的定义即可证出结论;
(3)连接AD、DF,根据三角形中线的性质可知S△ABF=S△BCF=2S△BCG,结合已知条件即可求出S△BCG=![]() ,再根据等高时,面积比等于底之比即可求出S△BDG=8,再根据三角形的面积公式即可求出结论.
,再根据等高时,面积比等于底之比即可求出S△BDG=8,再根据三角形的面积公式即可求出结论.
解:(1)∠A=∠DBE,理由如下
∵![]()
∴∠E=90°
∴∠DBE=180°-∠E-∠BDE=90°-∠BDE
∵![]()
∴∠A=180°-∠ACB-∠ABC=90°-∠ABC
∵![]()
∴∠A=∠DBE
(2)∵![]() 平分
平分![]() ,
,
∴∠ABF=∠EBF
∵![]()
∴∠A=180°-∠ABF-∠AFB=180°-∠EBF-∠EFB=∠FEB
由(1)知∠A=∠DBE
∴∠FEB=∠DBE
∴EF∥BD
∴∠EFC=∠ACB=90°,
∴![]() ;
;
(3)连接AD、DF
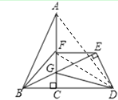
∵![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,
∴S△ABF=S△BCF=2S△BCG
∵![]()
∴S△ADF=![]() S△ABF=3S△BCG,BC:CD=
S△ABF=3S△BCG,BC:CD=![]() =2:3
=2:3
∴BC:BD=2:5
∵![]()
∴![]()
∴S△BCG=![]()
∵S△BCG:S△BDG=BC:BD
即![]() :S△BDG=2:5
:S△BDG=2:5
解得S△BDG=8
∴![]() BG·DE=8
BG·DE=8
∵![]()
∴![]() BG2=8
BG2=8
解得BG=4或-4(不符合实际,舍去)
即BG=4.