题目内容
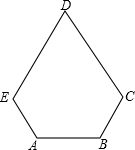 如图,凸五边形ABCDE中,∠A=∠B=120°,EA=AB=BC=
如图,凸五边形ABCDE中,∠A=∠B=120°,EA=AB=BC=| 1 |
| 2 |
| 1 |
| 2 |
| A、30° | B、45° |
| C、60° | D、67.5° |
分析:连接EC,不难得到四边形ABCE是等腰梯形,再根据∠A=∠B=120°可以推出EC=2AE,所以△EDC为等边三角形,∠D等于60°.
解答: 解:连接EC,易得梯形ABCE,
解:连接EC,易得梯形ABCE,
∵EA=AB=BC,且∠A=∠B=120°,
∴∠AEC=∠BCE=60°;
进而可得EC=2AE.
在△EDC中,
DC=DE=EC;
∴∠D=60°.
故选C.
 解:连接EC,易得梯形ABCE,
解:连接EC,易得梯形ABCE,∵EA=AB=BC,且∠A=∠B=120°,
∴∠AEC=∠BCE=60°;
进而可得EC=2AE.
在△EDC中,
DC=DE=EC;
∴∠D=60°.
故选C.
点评:本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
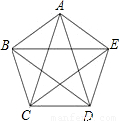
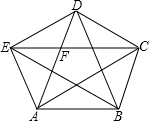 如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.
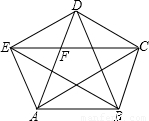
如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.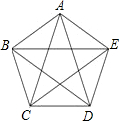 已知:如图,凸五边形ABCDE中,S△ABC=S△BCD=S△CDE=S△DEA=S△EAB=1,则S五边形ABCDE=
已知:如图,凸五边形ABCDE中,S△ABC=S△BCD=S△CDE=S△DEA=S△EAB=1,则S五边形ABCDE=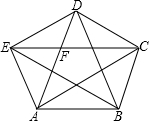 如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.
如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.