题目内容
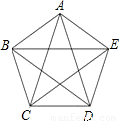
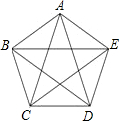已知：如图，凸五边形ABCDE中，S△ABC=S△BCD=S△CDE=S△DEA=S△EAB=1，则S五边形ABCDE=分析：先根据AB∥CF，BC∥AF得出ABCF为平行四边形，再根据△DEF∽△ACF，求出S△AEF的面积，即可求出五边形ABCDE的面积．
解答：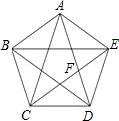
解：∵AB∥CF，BC∥AF，
∴，即S△ABC=S△ACF=1，
又∵AC∥DE，
∴△ACF∽△DEF
设S△AEF=x，则S△DEF=1-x，
∵△AEF的边AF与△DEF的边DF上的高相等，
∴
=
，
∵△DEF∽△ACF，
∴
=(
)2=
=1-x，
整理解得x=
，
故SABCDE=3S△ABC+S△AEF=
=
(5+
)．
故答案为：
(5+
)．
解：∵AB∥CF，BC∥AF，∴，即S△ABC=S△ACF=1，
又∵AC∥DE，
∴△ACF∽△DEF
设S△AEF=x，则S△DEF=1-x，
∵△AEF的边AF与△DEF的边DF上的高相等，
∴
| DF |
| AF |
| 1-x |
| x |
∵△DEF∽△ACF，
∴
| S△DEF |
| S△ACF |
| DF |
| AF |
| (1-x)2 |
| x2 |
整理解得x=
| ||
| 2 |
故SABCDE=3S△ABC+S△AEF=
5+
| ||
| 2 |
| 1 |
| 2 |
| 5 |
故答案为：
| 1 |
| 2 |
| 5 |
点评：本题考查的是三角形的面积及等积变换，解答此题的关键是根据已知条件判断出五边形ABCDE是正五边形，再根据相似三角形的性质进行解答，此题难度较大．
练习册系列答案
相关题目
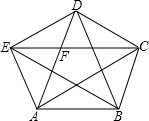如图，凸五边形ABCDE中，已知S△ABC=1，且EC∥AB，AD∥BC，BE∥CD，CA∥DE，DB∥EA．试求五边形ABCDE的面积．
