题目内容
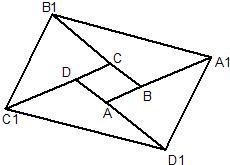8、如图，对面积为1的平行四边形ABCD逐次进行以下操作：第一次操作，分别延长AB，BC，CD，DA至点A1，B1，C1，D1，使得A1B=2AB，B1C=2BC，C1D=2CD，D1A=2AD，顺次连接A1，B1，C1，D1，得到平行四边形A1B1C1D1，记其面积为S1；第二次操作，分别延长A1B1，B1C1，C1D1、D1A1至点A2，B2，C2，D2，使得A2B1=2A1B1，B2C1=2B1C1，C2D1=2C1D1，D2A1=2A1D1，顺次连接A2，B2，C2，D2记其面积为S2；…；按此规律继续下去，可得到平行四边形A5B5C5D5，则其面积S5=135
．分析：根据题意分析可得：平行四边形ABCD的面积为1；每次操作后，每个三角形面积都是原平行四边形面积的3倍，所以新的平行四边形的面积就是原来平行四边形的13倍；按此规律继续下去，可得到平行四边形A5B5C5D5，则其面积S5=135．
解答：
解：如图，连接BD，B1D，
∵B1C=2BC，
∴△B1DC的面积是△DBC的面积的两倍，
又∵C1D=2DC，△B1C1D的面积是△B1DC的两倍，
∴△B1C1C的面积是△DBC的面积的三倍，
也就是平行四边形ABCD的面积的三倍，
以此类推，其余三个三角形的面积都是平行四边形面积的三倍，
∴新的平行四边形的面积是原来平行四边形面积的13倍，
按此规律继续下去，那么平行四边形A5B5C5D5的面积是135．
故填空答案135．
解：如图，连接BD，B1D，∵B1C=2BC，
∴△B1DC的面积是△DBC的面积的两倍，
又∵C1D=2DC，△B1C1D的面积是△B1DC的两倍，
∴△B1C1C的面积是△DBC的面积的三倍，
也就是平行四边形ABCD的面积的三倍，
以此类推，其余三个三角形的面积都是平行四边形面积的三倍，
∴新的平行四边形的面积是原来平行四边形面积的13倍，
按此规律继续下去，那么平行四边形A5B5C5D5的面积是135．
故填空答案135．
点评：本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．
练习册系列答案
相关题目
