题目内容
已知：如图，AB与⊙O相切于点C，OA=OB，⊙O的直径为4，AB=8．（1）求OB的长；
（2）求sinA的值．
分析：（1）先由OA=OB可知△OAB是等腰三角形，再根据切线的性质可知OC⊥AB，故可求出BC的长，再利用勾股定理求出OB的长即可．
（2）根据OA=OB求出OA的长，再根据角的三角函数值求出sinA的值即可．
（2）根据OA=OB求出OA的长，再根据角的三角函数值求出sinA的值即可．
解答：解：（1）由已知，OC=2，BC=4．
在Rt△OBC中，由勾股定理，得
OB=
=2
；
（2）在Rt△OAC中，
∵OA=OB=2
，OC=2，
∴sinA=
=
=
．
在Rt△OBC中，由勾股定理，得
OB=
| OC2+BC2 |
| 5 |
（2）在Rt△OAC中，
∵OA=OB=2
| 5 |
∴sinA=
| OC |
| OA |
| 2 | ||
2
|
| ||
| 5 |
点评：本题综合考查了切线的性质及直角三角形的性质、锐角三角函数的定义．
练习册系列答案
相关题目
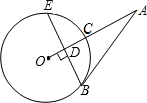已知，如图，AB与⊙O相切于点B，连接OA交⊙O于C，弦BE⊥OA于点D，AC=6，∠A=30°．
已知：如图，AB与CD相交于点O，∠ACO=∠BDO，OC=OD，CE是△ACO的角平分线．请你先作△ODB的角平分线DF（用尺规作图，不要求写出作法与证明，但要保留作图痕迹）；再证明CE=DF．
已知：如图，AB与DE相交于M，AC与DF相交于N，AB=AC，DE=DF，AD平分∠BAC．