题目内容
 已知:如图,AB与DE相交于M,AC与DF相交于N,AB=AC,DE=DF,AD平分∠BAC.
已知:如图,AB与DE相交于M,AC与DF相交于N,AB=AC,DE=DF,AD平分∠BAC.求证:AM=AN.
分析:首先根据等腰三角形的等边对等角得到∠ABC=∠ACB,∠E=∠F,从而得到∠EMB=∠FNC,然后再根据∠EMB=∠AMD,∠FNC=∠AND,得到∠AMD=∠AND,利用角平分线的性质得到MAD=∠NAD,从而证得△AMD≌△AND.
解答:证明:∵AB=AC,DE=DF,
∴∠ABC=∠ACB,∠E=∠F.(在一个三角形中,等边对等角).
∴∠EMB=∠FNC.
∵∠EMB=∠AMD,∠FNC=∠AND.
∴∠AMD=∠AND.
∵AD平分∠BAC,
∴MAD=∠NAD.
在△AMD和△AND中,
∴△AMD≌△AND(AAS).
∴AM=AN(全等三角形对应边相等).
∴∠ABC=∠ACB,∠E=∠F.(在一个三角形中,等边对等角).
∴∠EMB=∠FNC.

∵∠EMB=∠AMD,∠FNC=∠AND.
∴∠AMD=∠AND.
∵AD平分∠BAC,
∴MAD=∠NAD.
在△AMD和△AND中,
|
∴△AMD≌△AND(AAS).
∴AM=AN(全等三角形对应边相等).
点评:本题考查了全等三角形的判定及性质,同时还利用到了等腰三角形的性质,相对于其他知识,同学们对全等三角形掌握的相对比较好.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.
已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.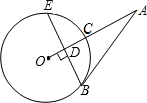 已知,如图,AB与⊙O相切于点B,连接OA交⊙O于C,弦BE⊥OA于点D,AC=6,∠A=30°.
已知,如图,AB与⊙O相切于点B,连接OA交⊙O于C,弦BE⊥OA于点D,AC=6,∠A=30°. 已知:如图,AB与CD相交于点O,∠ACO=∠BDO,OC=OD,CE是△ACO的角平分线.请你先作△ODB的角平分线DF(用尺规作图,不要求写出作法与证明,但要保留作图痕迹);再证明CE=DF.
已知:如图,AB与CD相交于点O,∠ACO=∠BDO,OC=OD,CE是△ACO的角平分线.请你先作△ODB的角平分线DF(用尺规作图,不要求写出作法与证明,但要保留作图痕迹);再证明CE=DF.