Question

【题目】以下四个命题中真命题是（ ）
①三角形有且只有一个内切圆；
②四边形的内角和与外角和相等；
③顺次连接四边形各边中点所得的四边形一定是菱形；
④一组对边平行且一组对角相等的四边形是平行四边形．
A.①②
B.③④
C.①②④
D.②③④

Answer 1

【答案】C
【解析】解：①三角形有且只有一个内切圆，正确；
②四边形的内角和与外角和相等，正确；
③顺次连接四边形各边中点所得的四边形一定是平行四边形，故此选项错误；
④一组对边平行且一组对角相等的四边形是平行四边形，正确，
理由：连接BD，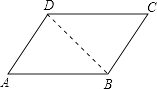

∵AB∥CD，
∴∠ABD=∠CDB，
在△ABD和△CDB中，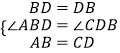
，
∴△ABD≌△CDB（SAS），
∴∠ADB=∠CBD，
∴AD∥BC．
又AB∥CD，
∴四边形ABCD是平行四边形．
故正确的有：①②④．
故选：C．
【考点精析】利用命题与定理对题目进行判断即可得到答案，需要熟知我们把题设、结论正好相反的两个命题叫做互逆命题．如果把其中一个叫做原命题，那么另一个叫做它的逆命题；经过证明被确认正确的命题叫做定理．