题目内容
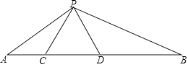
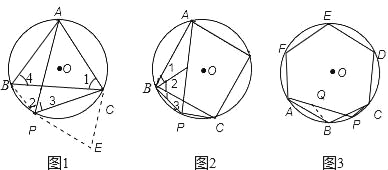
【题目】(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC.
下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.
证明:在AP上截取AE=CP,连接BE
∵△ABC是正三角形
∴AB=CB
∵∠1和∠2的同弧圆周角
∴∠1=∠2
∴△ABE≌△CBP
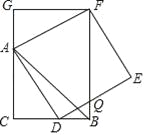
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:PA=PC+ ![]() PB.
PB.
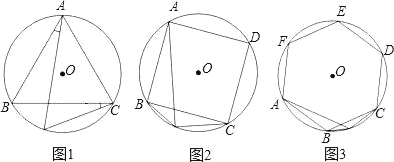
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.
【答案】(1)见解析;(2)见解析;(3)PA=PC+![]() PB
PB
【解析】
(1)延长BP至E,使PE=PC,连接CE,证明△PCE是等边三角形.利用CE=PC,∠E=∠3=60°,∠EBC=∠PAC,得到△BEC≌△APC,所以PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,证明ABE≌△CBP,所以PC=AE,可得PA=PC+![]() PB;(3)在AP上截取AQ=PC,连接BQ可证△ABQ≌△CBP,所以BQ=BP.又因为∠APB=30°.所以PQ=
PB;(3)在AP上截取AQ=PC,连接BQ可证△ABQ≌△CBP,所以BQ=BP.又因为∠APB=30°.所以PQ=![]() PB,PA=PQ+AQ=
PB,PA=PQ+AQ=![]() PB+PC.
PB+PC.
证明:(1)延长BP至E,使PE=PC,
连接CE.∵∠1=∠2=60°,∠3=∠4=60°,
∴∠CPE=60°,
∴△PCE是等边三角形,
∴CE=PC,∠E=∠3=60°;
又∵∠EBC=∠PAC,
∴△BEC≌△APC,
∴PA=BE=PB+PC.
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
又∵∠APB=45°,
∴BP=BE,∴;![]()
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴![]() .
.
(3)答:![]() ;
;
证明:在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
又∵∠APB=30°,
∴![]() PB
PB
∴![]() PB+PC
PB+PC

 名校课堂系列答案
名校课堂系列答案