题目内容
【题目】(本小题4分)(1)在图1中, 求∠A1+∠B1+∠C1+∠A2+∠B2+∠C2的度数= .
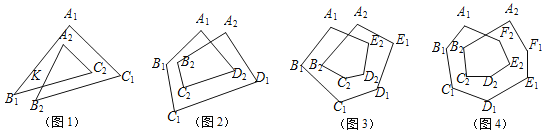
(2)我们作如下规定:
图1称为2环三角形,它的内角和为∠A1+∠B1+∠C1+∠A2+∠B2+∠C2;
图2为2环四边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2;
图3称为2环5五边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠E1+∠A2+∠B2+∠C2+∠D2+∠E2;
想一想:2环n边形的内角和为 度(只要求直接写出结论).
【答案】(1)360°;(2)(n-2)360°
【解析】
试题分析:(1)连结B1B2,首先根据三角形的内角和得到∠A2+∠C1=∠B1B2A2+∠B2B1C1,然后所求的六个角的和可转化为四边形A1B1B2C2的内角和;(2)2环n边形添加(n-2)条边,2环n边形的内角和成为(2n-2)边形的内角和,然后根据多边形的内角和公式计算即可.
试题解析:(1)连结B1B2,
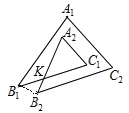
则∠A2+∠C1=∠B1B2A2+∠B2B1C1,
∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=∠A1+∠B1+∠B1B2A2+∠B2B1C1+∠B2+∠C2=360°;
(2)如图,A1A2之间添加两条边,
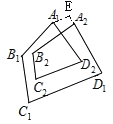
可得B2+∠C2+∠D2=∠EA1D+∠A1EA2+∠EA2B2
则∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2=∠A1+∠B1+∠C1+∠D1+∠A2+∠EA1D+∠A1EA2+∠EA2B2=720°;
2环n边形添加(n-2)条边,2环n边形的内角和成为(2n-2)边形的内角和.其内角和为(2n-4)180°=(n-2)360°.
故答案为:(1)360;(2)(n-2)360°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目