题目内容
【题目】如果P 是正方形ABCD 内的一点，且满足∠APB＋∠DPC＝180°，那么称点P 是正方形 ABCD 的“对补点”.
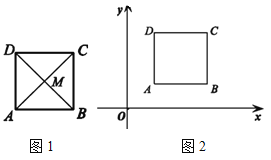
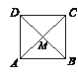
（1）如图1，正方形ABCD 的对角线AC，BD 交于点M，求证：点M 是正方形ABCD 的对补点；
（2）如图2，在平面直角坐标系中，正方形ABCD 的顶点A（1，1），C（3，3）.除对角线交点外，请再写出一个该正方形的对补点的坐标，并证明.
【答案】（1）证明见解析；
（2）对补点如：N（
， 
）．证明见解析
【解析】试题分析：(1)根据正方形的对角线互相垂直,得到∠DMC＝∠AMB＝90°,从而得到点M是正方形ABCD的对补点.(2) 在直线y＝x（1＜x＜3）或直线y＝－x＋4（1＜x＜3）上
除（2，2）外的任意点均可,通过证明△DCN≌△BCN,得到∠CND＝∠CNB,利用邻补角的性质即可得出结论.
试题解析：
（1）
∵四边形ABCD是正方形，
∴ AC⊥BD．
∴ ∠DMC＝∠AMB＝90°.
即 ∠DMC＋∠AMB＝180°．
∴ 点M是正方形ABCD的对补点．
（2）对补点如：N（
， 
）．
说明：在直线y＝x（1＜x＜3）或直线y＝－x＋4（1＜x＜3）上
除（2，2）外的任意点均可.
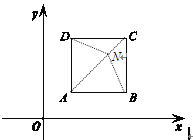
证明（方法一）：
连接AC ，BD
由（1）得此时对角线的交点为（2，2）．
设直线AC的解析式为：y＝kx＋b，
把点A（1，1），C（3，3）分别代入，
可求得直线AC的解析式为：y＝x．
则点N（
， 
）是直线AC上除对角线交点外的一点，且在正方形ABCD内.
连接AC，DN，BN，
∵ 四边形ABCD是正方形，
∴ DC＝BC，∠DCN＝∠BCN．
又∵ CN＝CN，
∴ △DCN≌△BCN．
∴ ∠CND＝∠CNB．
∵ ∠CNB＋∠ANB＝180°，
∴ ∠CND＋∠ANB＝180°．
∴ 点N是正方形ABCD的对补点．
证明（方法二）：
连接AC ，BD，
由（1）得此时对角线的交点为（2，2）．
设点N是线段AC上的一点（端点A，C及对角线交点除外），
连接AC，DN，BN，
∵ 四边形ABCD是正方形，
∴ DC＝BC，∠DCN＝∠BCN．
又∵ CN＝CN，
∴ △DCN≌△BCN．
∴ ∠CND＝∠CNB．
∵ ∠CNB＋∠ANB＝180°，
∴ ∠CND＋∠ANB＝180°．
∴ 点N是正方形ABCD除对角线交点外的补点．
设直线AC的解析式为：y＝kx＋b，
把点A（1，1），C（3，3）分别代入，可求得直线AC的解析式为：y＝x．
在1＜x＜3范围内，任取一点均为该正方形的对补点，如N（
， 
）．
