题目内容
若△ABC和△ADE均为等边三角形,M、N分别是BE、CD的中点.(1)当△ADE绕A点旋转到如图①的位置时,求证:CD=BE,△AMN是等边三角形;
(2)如图②,当∠EAB=30°,AB=12,AD=2
| 3 |
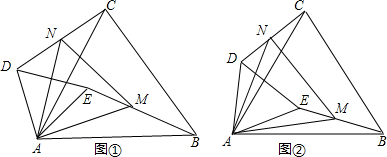
分析:(1)先证明△ABE≌△ACD(SAS),再证明△ABM≌△ACN(SAS),可得∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠CAB=60°,即可证明结论;
(2)作EF⊥AB于点F,可得EF=
,作MH⊥AB于点H,M是BE中点,得MH=
EF=
,在Rt△MPH中,利用勾股定理可求得.
(2)作EF⊥AB于点F,可得EF=
| 3 |
| 1 |
| 2 |
| ||
| 2 |
解答: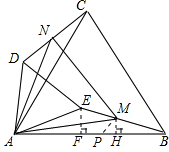 (1)证明:∵△ABC和△ADE均为等边三角形,
(1)证明:∵△ABC和△ADE均为等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=60°,
∵∠BAE=∠BAC-∠EAC,∠DAC=∠EAD-∠EAC,
∴∠BAE=∠DAC,
∴△ABE≌△ACD,∴CD=BE,∠ABE=∠ACD,
∵M、N分别是BE、CD的中点,即BM=
BE,CN=
CD,
∴BM=CN.又AB=AC,
∴△ABM≌△ACN,
∴AM=AN,∠MAB=∠NAC,
∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠CAB=60°,
∴△AMN是等边三角形.
(2)解:作EF⊥AB于点F,在Rt△AEF中,
∵∠EAB=30°,AE=AD=2
,
∴EF=
,
∵M是BE中点,作MH⊥AB于点H,
∴MH∥EF,MH=
EF=
,
取AB中点P,连接MP,则MP∥AE,MP=
AE,
∴∠MPH=30°,MP=
,
∴在Rt△MPH中,PH=
,
∴AH=AP+PH=
,
在Rt△AMH中,AM=
=
.
 (1)证明:∵△ABC和△ADE均为等边三角形,
(1)证明:∵△ABC和△ADE均为等边三角形,∴AB=AC,AE=AD,∠BAC=∠EAD=60°,
∵∠BAE=∠BAC-∠EAC,∠DAC=∠EAD-∠EAC,
∴∠BAE=∠DAC,
∴△ABE≌△ACD,∴CD=BE,∠ABE=∠ACD,
∵M、N分别是BE、CD的中点,即BM=
| 1 |
| 2 |
| 1 |
| 2 |
∴BM=CN.又AB=AC,
∴△ABM≌△ACN,
∴AM=AN,∠MAB=∠NAC,
∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠CAB=60°,
∴△AMN是等边三角形.
(2)解:作EF⊥AB于点F,在Rt△AEF中,
∵∠EAB=30°,AE=AD=2
| 3 |
∴EF=
| 3 |
∵M是BE中点,作MH⊥AB于点H,
∴MH∥EF,MH=
| 1 |
| 2 |
| ||
| 2 |
取AB中点P,连接MP,则MP∥AE,MP=
| 1 |
| 2 |
∴∠MPH=30°,MP=
| 3 |
∴在Rt△MPH中,PH=
| 3 |
| 2 |
∴AH=AP+PH=
| 15 |
| 2 |
在Rt△AMH中,AM=
| AH2+MH2 |
| 57 |
点评:本题考查了全等三角形的判定和性质、等边三角形的性质和勾股定理的应用,属综合性较强的题目,本题作好辅助线,构建含30°角的直角三角形是解答的关键.

练习册系列答案
相关题目


 (2012•台州模拟)已知A、B、C、D点的坐标如图所示,E在线段AC的延长线上,若△ABC和△ADE相似,则E点的坐标是
(2012•台州模拟)已知A、B、C、D点的坐标如图所示,E在线段AC的延长线上,若△ABC和△ADE相似,则E点的坐标是