题目内容
若等腰三角形一腰上的高和另一腰的夹角为28°,则该三角形的一个底角为
- A.59°
- B.31°
- C.59°或31°
- D.60°或30°
C
分析:等腰三角形一腰上的高与另一腰的夹角为28°,但没有明确此等腰三角形是锐角三角形还是钝角三角形,因此,有两种情况,需分类讨论.
解答: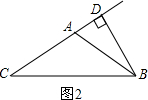
 解:当等腰三角形为锐角三角形时,如图1,
解:当等腰三角形为锐角三角形时,如图1,
由已知可知,∠ABD=28°,
又∵BD⊥AC,
∴∠A=62°,
∴∠ABC=∠C=59°.
当等腰三角形为钝角三角形时,如图2,
由已知可知,∠ABD=28°,
又∵BD⊥AC,
∴∠DAB=62°,
∴∠C=∠ABC=31°.
故该三角形的一个底角为59°或31°.
故选C.
点评:本题考查了等腰三角形的性质,解决与等腰三角形有关的问题,由于等腰所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错.正确分类是解答本题的关键.
分析:等腰三角形一腰上的高与另一腰的夹角为28°,但没有明确此等腰三角形是锐角三角形还是钝角三角形,因此,有两种情况,需分类讨论.
解答:

 解:当等腰三角形为锐角三角形时,如图1,
解:当等腰三角形为锐角三角形时,如图1,由已知可知,∠ABD=28°,
又∵BD⊥AC,
∴∠A=62°,
∴∠ABC=∠C=59°.
当等腰三角形为钝角三角形时,如图2,
由已知可知,∠ABD=28°,
又∵BD⊥AC,
∴∠DAB=62°,
∴∠C=∠ABC=31°.
故该三角形的一个底角为59°或31°.
故选C.
点评:本题考查了等腰三角形的性质,解决与等腰三角形有关的问题,由于等腰所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错.正确分类是解答本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
若等腰三角形一腰上的高等于腰长的一半,则这个三角形的底角为( )
| A、30° | B、75° | C、30°或60° | D、75°或15° |