题目内容
1×2+2×3+3×4+…+99×100
- A.223300
- B.333300
- C.443300
- D.433300
B
分析:根据n(n+1)=n2+n,再根据12+22+32+…+992=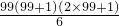 ;1+2+3+…+99=
;1+2+3+…+99= 计算即可.
计算即可.
解答:1×2+2×3+3×4+…+99×100
=(12+1)+(22+2)+(32+3)+…+(992+99)
=(12+22+32+…+992)+(1+2+3+…+99)
=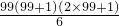 +
+
=333300
故选B.
点评:解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律.
分析:根据n(n+1)=n2+n,再根据12+22+32+…+992=
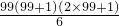 ;1+2+3+…+99=
;1+2+3+…+99= 计算即可.
计算即可.解答:1×2+2×3+3×4+…+99×100
=(12+1)+(22+2)+(32+3)+…+(992+99)
=(12+22+32+…+992)+(1+2+3+…+99)
=
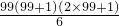 +
+
=333300
故选B.
点评:解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某公园门票价格如下表,有27名中学生游公园,则最少应付费________元.(游客只能在公园售票处购票)
| 购票张数 | 1~29张 | 30~60张 | 60张以上 |
| 每张票的价格 | 10元 | 8元 | 6元 |
 桌上摆着一个由若干相同的正方体组成的几何体,其正视图和左视图如图所示,那么这个几何体最多可以由个这样的正方体组成.
桌上摆着一个由若干相同的正方体组成的几何体,其正视图和左视图如图所示,那么这个几何体最多可以由个这样的正方体组成.