题目内容
【题目】如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,点M运动的路径长为 . 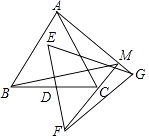
【答案】4π
【解析】解:如图,连接AD、DG.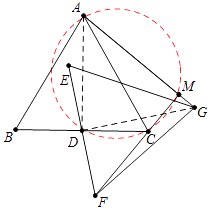
∵△ABC,△EFG均是边长为2的等边三角形,BD=CD,DE=DF,
∴AD⊥BC,GD⊥EF,
∴∠ADC=∠GDF=90°,
∴∠ADG=∠CDF,
∵AD=AG,DC=DF,
∴∠DAG=∠DGA=∠DCF=∠DFC,
∵∠DCF+∠DCM=180°,
∴∠DAM+∠DCM=180°,
∴∠ADC+∠AMC=180°,
∴∠AMC=90°,
∴点M的轨迹是以AC为直径的圆,
∴点M运动的路径长为4π,
所以答案是4π.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目