题目内容
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上.若点
轴的正半轴上.若点![]() ,
,![]() 在线段
在线段![]() 上,且
上,且![]() 为某个一边与
为某个一边与![]() 轴平行的矩形的对角线,则称这个矩形为点
轴平行的矩形的对角线,则称这个矩形为点![]() 、
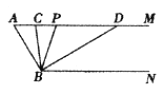
、![]() 的“涵矩形”.下图为点
的“涵矩形”.下图为点![]() ,
,![]() 的“涵矩形”的示意图.
的“涵矩形”的示意图.
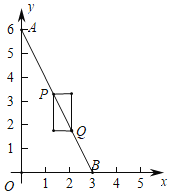
(1)点![]() 的坐标为
的坐标为![]() .
.
①若点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 与点
与点![]() 重合,则点
重合,则点![]() 、
、![]() 的“涵矩形”的周长为__________.
的“涵矩形”的周长为__________.
②若点![]() ,
,![]() 的“涵矩形”的周长为
的“涵矩形”的周长为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() ,
,![]() ,
,![]() 中,能够成为点
中,能够成为点![]() 、
、![]() 的“涵矩形”的顶点的是_________.
的“涵矩形”的顶点的是_________.
(2)四边形![]() 是点
是点![]() 、
、![]() 的“涵矩形”,点
的“涵矩形”,点![]() 在
在![]() 的内部,且它是正方形.
的内部,且它是正方形.
①当正方形![]() 的周长为
的周长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() 时,求点的坐标.
时,求点的坐标.
②当正方形![]() 的对角线长度为
的对角线长度为![]() 时,连结
时,连结![]() .直接写出线段
.直接写出线段![]() 的取值范围.
的取值范围.
【答案】(1)①![]() . ②
. ②![]() ;(2)①点
;(2)①点![]() 的坐标为
的坐标为![]() 或
或![]() .②
.②![]() .
.
【解析】
(1)①利用A、B的坐标求出直线AB的解析式,再将P点横坐标代入,计算即可得点![]() 、
、![]() 的“新矩形”的周长;②由直线AB的解析式判定是否经过E、F、G三点,发现只经过了F(1,2),能够成为点
的“新矩形”的周长;②由直线AB的解析式判定是否经过E、F、G三点,发现只经过了F(1,2),能够成为点![]() 、
、![]() 的“涵矩形”的顶点的是F(1,2)
的“涵矩形”的顶点的是F(1,2)
(2)①①根据正方形的性质可得出∠ABO=45°,结合点A的坐标可得出点B的坐标及直线AB的函数表达式,由![]() 的横坐标为
的横坐标为![]() ,可得出点P的坐标,再由正方形的周长可得出点Q的坐标,进而可得出点Q的坐标;②由正方形的对角线长度为
,可得出点P的坐标,再由正方形的周长可得出点Q的坐标,进而可得出点Q的坐标;②由正方形的对角线长度为![]() ,可得正方形的边长为1,由直线AB的解析式y=-x+6可知M点的运动轨迹是直线y=-x+5,由点
,可得正方形的边长为1,由直线AB的解析式y=-x+6可知M点的运动轨迹是直线y=-x+5,由点![]() 在
在![]() 的内部,x的取值范围是0<x<5,OM<5,OM最小值是由O向直线y=-x+5作垂线段,此时OM=
的内部,x的取值范围是0<x<5,OM<5,OM最小值是由O向直线y=-x+5作垂线段,此时OM=![]() ,可得OM的取值范围.
,可得OM的取值范围.
(1)①解:由A(0,6),B(3,0)可得直线AB的解析式为:y=-2x+6,
∵P点横坐标是![]()
∴当x=![]() 时,y=3
时,y=3
∴P(![]() ,3).
,3).
∵ 点![]() 与点
与点![]() 重合,
重合,
∴Q(3,0)
∴点![]() 、
、![]() 的“涵矩形”的宽为:3-
的“涵矩形”的宽为:3-![]() =
=![]() ,长为3-0=3
,长为3-0=3
∴点![]() 、
、![]() 的“涵矩形”的周长为:
的“涵矩形”的周长为:![]()
故答案为:9
②.由①可得直线AB的解析式为:y=-2x+6可设Q(a,-2a+6),则成为点![]() 、
、![]() 的“涵矩形”的顶点且在
的“涵矩形”的顶点且在![]() AOB内部的一点坐标为M(1,-2a+6)
AOB内部的一点坐标为M(1,-2a+6)
∴PM=4-(-2a+6)=2a-2,MQ=a-1
∵点![]() ,
,![]() 的“涵矩形”的周长为
的“涵矩形”的周长为![]()
∴PM+MQ=3
∴2a-2+a-1=3
解得:a=2
∴M(1,2)
故答案为:F(1,2),只写![]() 或
或![]() 也可以.
也可以.
(2)①![]() 点
点![]() 、
、![]() 的“涵矩形”是正方形,
的“涵矩形”是正方形,
![]()
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() 点
点![]() 的坐标为 ,
的坐标为 ,
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 正方形
正方形![]() 的周长为
的周长为![]() ,
,
![]() 点
点![]() 的横坐标为
的横坐标为![]() 或
或![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
②∵正方形的对角线长度为![]() ,
,
∴可得正方形的边长为1,
因为直线AB的解析式y=-x+6可设M点的运动轨迹是直线y=-x+b,且过(0,5)
故M点的运动轨迹是直线y=-x+5
∵点![]() 在
在![]() 的内部,x的取值范围是0<x<5,
的内部,x的取值范围是0<x<5,
∴当M落在OB或者OA边上时,OM取得最大值,此时OM=5,由于点![]() 在
在![]() 的内部,
的内部,
∴OM<5,
当OM⊥直线y=-x+5时,OM取得最小值,此时OM=![]() ,
,
∴OM的取值范围.![]() .
.
故答案为:![]()

【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).