题目内容
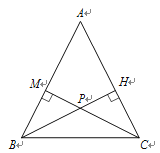
【题目】如图,在△ABC中,AB=AC,△ABC的高BH,CM交于点P.
(1)求证:PB=PC.
(2)若PB=5,PH=3,求AB.
【答案】(1)见解析;(2)10.
【解析】
(1)根据等边对等角可得∠ABC=∠ACB,根据三角形内角和定理可得∠MBP=∠HCP,然后可得∠PBC=∠PCB,可证PB=PC;
(2)利用AAS可直接证明△PMB≌△PHC,得到PM=PH=3,BM=CH,然后求出BM,在直角△ABH中利用勾股定理构建方程求出AM即可解决问题.
解:(1)∵AB=AC,
∴∠ABC=∠ACB,
又∵∠PMB=∠PHC=90°,∠MPB=∠HPC,
∴∠MBP=∠HCP,
∴∠ABC-∠MBP =∠ACB-∠HCP,即∠PBC=∠PCB,
∴PB=PC;
(2)在△PMB和△PHC中, ,
,
∴△PMB≌△PHC(AAS),
∴PM=PH=3,BM=CH,
∴BM=![]() ,AM=AH,
,AM=AH,
在Rt△ABH中,AB2=AH2+BH2,
∴(4+AM)2= AH2+(5+3)2,即(4+AM)2= AM2+82,
解得:AM=6,
∴AB=AM+BM=6+4=10.

练习册系列答案
相关题目
【题目】弹簧挂上物体后会伸长,若一弹簧长度(cm)与所挂物体质量(kg)之间的关系如下表:
物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
则下列说法错误的是( )
A.弹簧长度随物体的质量的变化而变化,物体的质量是自变量,弹簧的长度是因变量
B.如果物体的质量为x kg,那么弹簧的长度y cm可以表示为y=12+0.5x
C.在弹簧能承受的范围内,当物体的质量为7kg时,弹簧的长度为16cm
D.在没挂物体时,弹簧的长度为12cm