题目内容
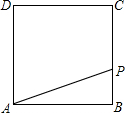
如图①,在梯形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向不停移动,直到点P到达点D后才停止.已知△PAD的面积S(单位:cm2)与点P移动的时间t(单位:s)的函数关系式如图②所示,则点P从开始移动到停止移动一共用了多少秒?(结果保留根号).


由图②可知,t在2到4秒时,△PAD的面积不发生变化,
∴在AB上运动的时间是2秒,在BC上运动的时间是4-2=2秒,
∵动点P的运动速度是1cm/s,
∴AB=2cm,BC=2cm,
过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,
则四边形BCFE是矩形,
∴BE=CF,BC=EF=2cm,
∵∠A=60°,
∴BE=ABsin60°=2×
=
,
AE=ABcos60°=2×
=1,
∴
×AD×BE=3
,
即
×AD×
=3
,
解得AD=6cm,
∴DF=AD-AE-EF=6-1-2=3,
在Rt△CDF中,CD=
=
=2
,
所以,动点P运动的总路程为AB+BC+CD=2+2+2
=4+2
,
∵动点P的运动速度是1cm/s,
∴点P从开始移动到停止移动一共用了(4+2
)÷1=4+2
(秒).
答:点P从开始移动到停止移动一共用了(4+2
)秒.

∴在AB上运动的时间是2秒,在BC上运动的时间是4-2=2秒,
∵动点P的运动速度是1cm/s,
∴AB=2cm,BC=2cm,
过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,
则四边形BCFE是矩形,
∴BE=CF,BC=EF=2cm,
∵∠A=60°,
∴BE=ABsin60°=2×
| ||
| 2 |
| 3 |
AE=ABcos60°=2×
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 3 |
即
| 1 |
| 2 |
| 3 |
| 3 |
解得AD=6cm,
∴DF=AD-AE-EF=6-1-2=3,
在Rt△CDF中,CD=
| CF2+DF2 |
| 3+9 |
| 3 |
所以,动点P运动的总路程为AB+BC+CD=2+2+2
| 3 |
| 3 |
∵动点P的运动速度是1cm/s,
∴点P从开始移动到停止移动一共用了(4+2
| 3 |
| 3 |
答:点P从开始移动到停止移动一共用了(4+2
| 3 |


练习册系列答案
相关题目