题目内容
【题目】某学校游戏节活动中,设计了一个有奖转盘游戏,如图,A转盘被分成三个面积相等的扇形,B转盘被分成四个面积相等的扇形,每一个扇形都标有相应的数字,先转动A转盘,记下指针所指区域内的数字,再转动B转盘,记下指针所指区域内的数字(当指针在边界线上时,重新转动转盘,直到指针指向一个区域内为止)
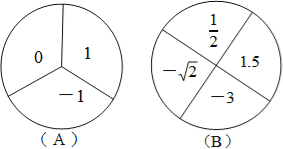
(1)请利用画树状图或列表的方法(只选其中一种),表示出转转盘可能出现的所有结果;
(2)如果将两次转转盘指针所指区域的数据相乘,乘积是无理数时获得一等奖,那么获得一等奖的概率是多少?
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;本题用列表法得出所有等可能的情况,进而可得转转盘可能出现的所有结果;
(2)无理数是无限不循环小数,找出乘积为无理数的情况数,再除以所有等可能出现的结果数,即可求出一等奖的概率.
(1)由题意列表如下,

由列表得知:当A转盘出现0,1,-1时,B转盘分别可能有4种等可能情况,
所以共有4×3=12种等可能情况.
即(0,![]() )、(0,1.5)、(0,-3)、(0,﹣
)、(0,1.5)、(0,-3)、(0,﹣![]() )、(1,
)、(1,![]() )、(1,1.5)、(1,-3)、(1,﹣
)、(1,1.5)、(1,-3)、(1,﹣![]() )、(-1,
)、(-1,![]() )、(-1,1.5)、(-1,-3)、(-1,﹣
)、(-1,1.5)、(-1,-3)、(-1,﹣![]() ).
).
(2)无理数是无限不循环小数,由列表得知:乘积是无理数的情况有2种,即(1,﹣![]() )、(-1,﹣
)、(-1,﹣![]() ).乘积分别是﹣
).乘积分别是﹣![]() ,
,![]() ,
,
∴P(乘积为无理数)=![]() =
=![]() .即P(获得一等奖)=
.即P(获得一等奖)=![]() .
.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目