题目内容
 如图,小岛A在港口P的南偏西45°方向,距离港口70海里处.甲船从A出发,沿AP方向以每小时20海里的速度驶向港口P;乙船从港口P出发,沿着南偏东60°方向,以每小时15海里的速度驶离港口.若两船同时出发.
如图,小岛A在港口P的南偏西45°方向,距离港口70海里处.甲船从A出发,沿AP方向以每小时20海里的速度驶向港口P;乙船从港口P出发,沿着南偏东60°方向,以每小时15海里的速度驶离港口.若两船同时出发.(1)几小时后两船与港口P的距离相等?
(2)几小时后乙船在甲船的正东方向?
(最后结果保留一位小数,参考数据:
| 2 |
| 3 |
分析:(1)首先设经过x小时后,两船距离港口距离相等,则甲船行驶的距离为20x海里,甲船行驶的距离为15x海里,即可得方程:70-20x=15x,解此方程即可求得答案;
(2)设经过y小时后,乙船在甲船的正东方向,由三角函数可求得在Rt△PBD中,PD=PB÷tan45°=
×(70-20y),在Rt△PDC中,PD=PC×cos60°=
×15y,继而可得方程
×(70-20y)=
×15y,解此方程即可求得答案.
(2)设经过y小时后,乙船在甲船的正东方向,由三角函数可求得在Rt△PBD中,PD=PB÷tan45°=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答:解:(1)设经过x小时后,两船距离港口距离相等,
则甲船行驶的距离为20x海里,甲船行驶的距离为15x海里,
∴甲与港口P是距离是(70-20x)海里;
由题意得:70-20x=15x,
解得:x=2,
∴两小时后两船距离港口的距离相等;
 (2)设经过y小时后,乙船在甲船的正东方向,
(2)设经过y小时后,乙船在甲船的正东方向,
∴此时点B距离P点(70-20y)海里,PC=15y海里,
在Rt△PBD中,PB=PD÷cos45°=
×(70-20y)(海里),
在Rt△PDC中,PD=PC×cos60°=
×15y(海里),
∴
×(70-20y)=
×15y,
解得:y=
≈2.3,
答:大约2.3小时后乙船在甲船的正东方向.
则甲船行驶的距离为20x海里,甲船行驶的距离为15x海里,
∴甲与港口P是距离是(70-20x)海里;
由题意得:70-20x=15x,
解得:x=2,
∴两小时后两船距离港口的距离相等;
 (2)设经过y小时后,乙船在甲船的正东方向,
(2)设经过y小时后,乙船在甲船的正东方向,∴此时点B距离P点(70-20y)海里,PC=15y海里,
在Rt△PBD中,PB=PD÷cos45°=
| ||
| 2 |
在Rt△PDC中,PD=PC×cos60°=
| 1 |
| 2 |
∴
| ||
| 2 |
| 1 |
| 2 |
解得:y=
112-52
| ||
| 23 |
答:大约2.3小时后乙船在甲船的正东方向.
点评:此题考查了方向角问题.此题难度适中,注意掌握辅助线的作法,注意构造直角三角形,并利用解直角三角形的知识求解是解此题的关键.

练习册系列答案
相关题目
 AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发.
AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发.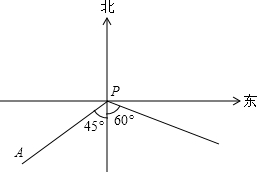
 正东方向?(结果保留根号)
正东方向?(结果保留根号)
 ≈1.41,
≈1.41,