题目内容
如图,小岛A在港口P的南偏西45°方向,距离港口100海里处,甲船从A出发,沿AP方向以10海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向以20海里/时的速度驶离港口.现两船同时出发,出发后几小时乙船在甲船的 正东方向?(结果保留根号)
正东方向?(结果保留根号)
分析:本题中如果设此时甲船在点B处,乙船在点C处,连接BC交P的正南方于Q,那么我们可发现PQ是直角三角形PQB和PQC的公共边,可用时间表示出PB和PC的长,然后根据PQ在不同直角三角形中不同的表达式,来求出时间.
解答: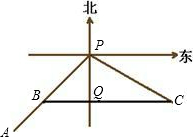 解:设出发t小时后乙船在甲船的正东方向,此时甲船在点B处,乙船在点C处,
解:设出发t小时后乙船在甲船的正东方向,此时甲船在点B处,乙船在点C处,
连接CB在P正南方向取点Q,则PQ⊥BC于Q,据题意:
在Rt△PQB中,∠BPQ=45°,∴PQ=BPcos45°=
(100-10t)
在Rt△PQC中,∠CPQ=60°,∴PQ=PCcos60°=
×20t=10t,
∴
(100-10t)=10t,
∴t=
=10
-10.
解得:t=
=10
-10(时).
 解:设出发t小时后乙船在甲船的正东方向,此时甲船在点B处,乙船在点C处,
解:设出发t小时后乙船在甲船的正东方向,此时甲船在点B处,乙船在点C处,连接CB在P正南方向取点Q,则PQ⊥BC于Q,据题意:
在Rt△PQB中,∠BPQ=45°,∴PQ=BPcos45°=
| ||
| 2 |
在Rt△PQC中,∠CPQ=60°,∴PQ=PCcos60°=
| 1 |
| 2 |
∴
| ||
| 2 |
∴t=
| 10 | ||
1+
|
| 2 |
解得:t=
| 10 | ||
1+
|
| 2 |
点评:本题的关键是要构建出与已知条件和问题相关的直角三角形,然后依据公共直角边来求解.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发.
AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发.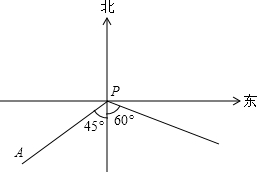
 如图,小岛A在港口P的南偏西45°方向,距离港口70海里处.甲船从A出发,沿AP方向以每小时20海里的速度驶向港口P;乙船从港口P出发,沿着南偏东60°方向,以每小时15海里的速度驶离港口.若两船同时出发.
如图,小岛A在港口P的南偏西45°方向,距离港口70海里处.甲船从A出发,沿AP方向以每小时20海里的速度驶向港口P;乙船从港口P出发,沿着南偏东60°方向,以每小时15海里的速度驶离港口.若两船同时出发.
 ≈1.41,
≈1.41,