题目内容
18、点P是△ABC中AB边上的一点，过点P作直线（不与直线AB重合）截△ABC，使截得的三角形与△ABC相似．满足这样条件的直线最多有
4
条．分析：过点P作BC的平行线，作AC的平行线，都可使截得的三角形与原三角形相似；过点P可作直线交边AC于点E，使得AP：AC=AE：AB，可得△APE∽△ACB，同理截BC边也可得相似三角形．
解答：
解：过P作PE∥BC，则△APE∽ABC；
同理：△BPE∽△BAC；
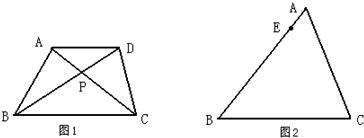
过P作PA：AC=AE：AB，则△APE∽△ACB；
同理：△BPE∽△BCA；
故共有4条．
解：过P作PE∥BC，则△APE∽ABC；同理：△BPE∽△BAC；
过P作PA：AC=AE：AB，则△APE∽△ACB；
同理：△BPE∽△BCA；
故共有4条．
点评：此题考查了相似三角形的判定：
①有两个对应角相等的三角形相似；
②有两个对应边的比相等，且其夹角相等，则两个三角形相似；
③三组对应边的比相等，则两个三角形相似．
①有两个对应角相等的三角形相似；
②有两个对应边的比相等，且其夹角相等，则两个三角形相似；
③三组对应边的比相等，则两个三角形相似．
练习册系列答案
相关题目
