Question

（1997•河南）已知等腰梯形的高是3cm，它的中位线长是6cm，一个底角是45°，那么这个梯形的下底边的长是

9

cm．

Answer 1

分析：GH是等腰梯形的中位线，作AE⊥BC，DF⊥BC，则四边形ADFE是矩形，△ABE，△DCF是等腰直角三角形，由梯形的中位线的性质可求得上下底的长．

解答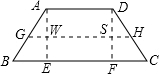：解：如图，GH是等腰梯形的中位线，作AE⊥BC，DF⊥BC，则四边形ADFE是矩形，
有AD=EF，AE=DF=3，
∵∠B=∠C=45°，AE⊥BC，DF⊥BC
∴△ABE，△DCF是等腰直角三角形，
∴AE=BE=CF，
∵GH是等腰梯形的中位线
∴AD+BC=BC+EF=2AE+2AD=2GH=12，
∴AD=EF=3，BC=9，
故答案为：9；

点评：本题利用了等腰直角三角形的判定和性质，梯形的中位线的性质．