题目内容
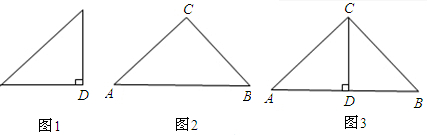
 22、如图,是两个形状、大小完全一样的三角板,请将它们拼接成一个几何图形,使得这两个三角板有一边完全重合或一边部分重合,且拼接成的图形中有两组平行线.画出你所设计的图形,写出这两组平行线并说明平行的理由.
22、如图,是两个形状、大小完全一样的三角板,请将它们拼接成一个几何图形,使得这两个三角板有一边完全重合或一边部分重合,且拼接成的图形中有两组平行线.画出你所设计的图形,写出这两组平行线并说明平行的理由.分析:有两组平行线,那么相等的角应组成这两组平行线的内错角.
解答:解:
∵∠BAC=∠DEF
∴BC∥EF,
同理可得到AC∥FD.

∵∠BAC=∠DEF
∴BC∥EF,
同理可得到AC∥FD.
点评:本题考查学生的动手操作能力;应用的知识点为;内错角相等,两直线平行.

练习册系列答案
相关题目
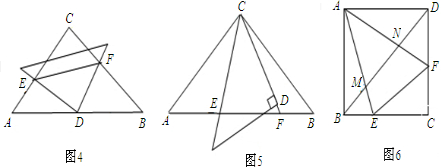
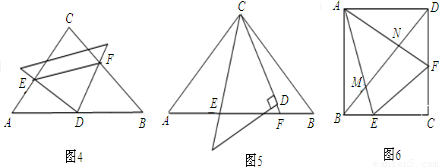
 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.

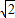 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.

 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
