题目内容
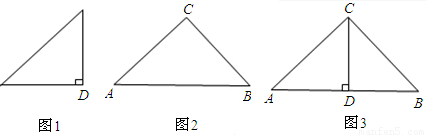
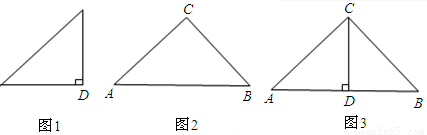
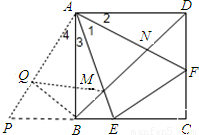
如图1、2是两个相似比为1: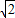 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
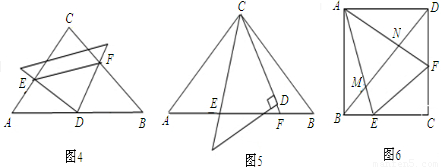
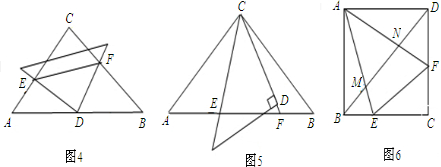
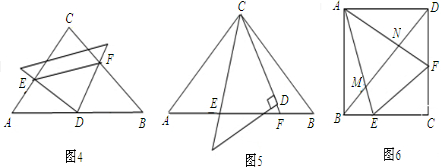
的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.(1)在图3中,绕点D旋转小直角三角形,使两直角边分别与AC、BC交于点E,F,如图4.求证:AE2+BF2=EF2;
(2)若在图3中,绕点C旋转小直角三角形,使它的斜边和CD延长线分别与AB交于点E、F,如图5,此时结论AE2+BF2=EF2是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(3)如图6,在正方形ABCD中,E、F分别是边BC、CD上的点,满足△CEF的周长等于正方形ABCD的周长的一半,AE、AF分别与对角线BD交于M、N,试问线段BM、MN、DN能否构成三角形的三边长?若能,指出三角形的形状,并给出证明;若不能,请说明理由.
【答案】分析:(1)连CD,由条件得到点D为AB的中点,则CD=AD,∠4=∠A=45°,易证△CDF≌△ADE,△CED≌△BFD,得到CF=AE,CE=BF,而CE2+CF2=EF2,因此得到结论.
(2)把△CFB绕点C顺时针旋转90°,得到△CGA,根据旋转的性质得到CF=CG,AG=BF,∠4=∠1,∠B=∠GAC=45°,易证△CGE≌△CFE,得到GE=EF,即可得到结论AE2+BF2=EF2仍然成立;
(3)把△ADF绕点A顺时针旋转90°得到△ABP,点N的对应点为Q,根据旋转的性质得到∠4=∠2,∠1+∠3+∠4=90°,BP=DF,BQ=CN,AF=AP,又△CEF的周长等于正方形ABCD的周长的一半,得到EF=BE+DF,则EF=EP,证得△AMQ≌△AMN,得到MN=QM,易证得∠QBN=90°,于是有BQ2+BM2=QM2,从而得到BM2+DN2=MN2.
解答:证明:(1)连CD,如图4,
∵两个等腰直角三角形的相似比为1: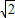 ,
,
而小直角三角形的斜边等于大直角三角形的直角边,

∴点D为AB的中点,
∴CD=AD,∠4=∠A=45°,
又∵∠1+∠2=∠2+∠3=90°,
∴∠3=∠1,
∴△CDF≌△ADE,
∴CF=AE,
同理可得△CED≌△BFD,
∴CE=BF,
而CE2+CF2=EF2,
∴AE2+BF2=EF2;
(2)结论AE2+BF2=EF2仍然成立.理由如下:
把△CFB绕点C顺时针旋转90°,得到△CGA,如图5
∴CF=CG,AG=BF,∠4=∠1,∠B=∠GAC=45°,
∴∠GAE=90°,
而∠3=45°,
∴∠2+∠4=90°-45°=45°,
∴∠1+∠2=45°,
∴△CGE≌△CFE,
∴GE=EF,
在Rt△AGE中,AE2+AG2=GE2,
∴AE2+BF2=EF2;
(3)线段BM、MN、DN能构成直角三角形的三边长.理由如下:
把△ADF绕点A顺时针旋转90°得到△ABP,点N的对应点为Q,如图
∴∠4=∠2,∠1+∠3+∠4=90°,BP=DF,BQ=DN,AF=AP,
∵△CEF的周长等于正方形ABCD的周长的一半,
∴EF=BE+DF,
∴EF=EP,
∴△AEF≌△AEP,
∴∠1=∠3+∠4,
而AQ=AN,
∴△AMQ≌△AMN,
∴MN=QM,
而∠ADN=∠QBA=45°,∠ABD=45°,
∴∠QBN=90°,
∴BQ2+BM2=QM2,
∴BM2+DN2=MN2.
点评:本题考查了旋转的性质:旋转前后两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角;也考查了三角形全等的判定与性质、等腰直角三角形的性质以及勾股定理的应用.
(2)把△CFB绕点C顺时针旋转90°,得到△CGA,根据旋转的性质得到CF=CG,AG=BF,∠4=∠1,∠B=∠GAC=45°,易证△CGE≌△CFE,得到GE=EF,即可得到结论AE2+BF2=EF2仍然成立;
(3)把△ADF绕点A顺时针旋转90°得到△ABP,点N的对应点为Q,根据旋转的性质得到∠4=∠2,∠1+∠3+∠4=90°,BP=DF,BQ=CN,AF=AP,又△CEF的周长等于正方形ABCD的周长的一半,得到EF=BE+DF,则EF=EP,证得△AMQ≌△AMN,得到MN=QM,易证得∠QBN=90°,于是有BQ2+BM2=QM2,从而得到BM2+DN2=MN2.
解答:证明:(1)连CD,如图4,
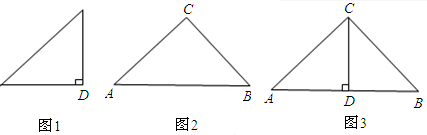
∵两个等腰直角三角形的相似比为1:
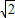 ,
,而小直角三角形的斜边等于大直角三角形的直角边,

∴点D为AB的中点,
∴CD=AD,∠4=∠A=45°,
又∵∠1+∠2=∠2+∠3=90°,
∴∠3=∠1,
∴△CDF≌△ADE,
∴CF=AE,
同理可得△CED≌△BFD,
∴CE=BF,
而CE2+CF2=EF2,
∴AE2+BF2=EF2;
(2)结论AE2+BF2=EF2仍然成立.理由如下:
把△CFB绕点C顺时针旋转90°,得到△CGA,如图5
∴CF=CG,AG=BF,∠4=∠1,∠B=∠GAC=45°,
∴∠GAE=90°,
而∠3=45°,
∴∠2+∠4=90°-45°=45°,
∴∠1+∠2=45°,
∴△CGE≌△CFE,
∴GE=EF,
在Rt△AGE中,AE2+AG2=GE2,
∴AE2+BF2=EF2;
(3)线段BM、MN、DN能构成直角三角形的三边长.理由如下:
把△ADF绕点A顺时针旋转90°得到△ABP,点N的对应点为Q,如图

∴∠4=∠2,∠1+∠3+∠4=90°,BP=DF,BQ=DN,AF=AP,
∵△CEF的周长等于正方形ABCD的周长的一半,
∴EF=BE+DF,
∴EF=EP,
∴△AEF≌△AEP,
∴∠1=∠3+∠4,
而AQ=AN,
∴△AMQ≌△AMN,
∴MN=QM,
而∠ADN=∠QBA=45°,∠ABD=45°,
∴∠QBN=90°,
∴BQ2+BM2=QM2,
∴BM2+DN2=MN2.
点评:本题考查了旋转的性质:旋转前后两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角;也考查了三角形全等的判定与性质、等腰直角三角形的性质以及勾股定理的应用.

练习册系列答案
相关题目
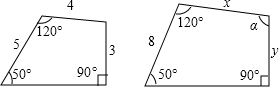
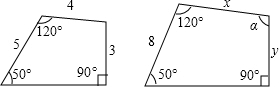 如图所示,是两个相似四边形,则x=
如图所示,是两个相似四边形,则x= 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.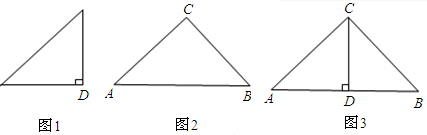
 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.