Question

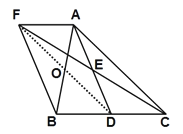
【题目】如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作AF//BC，交CE的延长线于点F，且AF=BD，连接BF．

（1）BD与CD有什么数量关系，并说明理由．

（2）连接FD，与AB相交于点O，若BO=AC，试判断四边形AFBD的形状，并证明你的结论．

Answer 1

【答案】（1）BD=CD，理由见解析；（2）四边形AFBD是矩形，证明见解析.

【解析】

（1）先证明△AFE≌△DCE，从而得到AF=CD，因为AF=BD，则结论得证；

（2）先证明四边形AFBD是平行四边形，再等腰三角形的利用三线合一证得AD⊥BC，即∠ADB=90,即可证得四边形AFBD是矩形.

（1）BD=CD，理由为：

∵AF∥BC,

∴∠AFE=∠DCE,

∵E是AD的中点,

∴AE=ED,

又∠AEF=∠DEC,

∴△AFE≌△DCE,

∴AF=CD,

∵AF=BD,

∴BD=CD；

（2）四边形AFBD是矩形.理由为：

∵AF∥BC，AF=BD,

∴四边形AFBD是平行四边形，

∴BO=AB,

∵BO=AC

∴ AB=AC，

∵BD=CD，

∴AD⊥BC，即∠ADB=90，

∴四边形AFBD是矩形.