题目内容
(本小题满分9分)
已知关于 的方程
的方程 有两个不相等的实数根
有两个不相等的实数根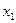 、
、 ,问是否存在实数
,问是否存在实数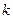 ,使方程的两实数根互为相反数?如果存在,求出
,使方程的两实数根互为相反数?如果存在,求出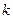 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
已知关于
 的方程
的方程 有两个不相等的实数根
有两个不相等的实数根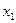 、
、 ,问是否存在实数
,问是否存在实数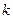 ,使方程的两实数根互为相反数?如果存在,求出
,使方程的两实数根互为相反数?如果存在,求出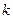 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。两根互为相反数
∴两根之和等于0
即-(K+2)/k=0
k=-2
当k=-2时原方程可化为
-2x²-2=0
x²+1=0
无解
∴不存在相应的k值,使两根互为相反数
赞同
∴两根之和等于0
即-(K+2)/k=0
k=-2
当k=-2时原方程可化为
-2x²-2=0
x²+1=0
无解
∴不存在相应的k值,使两根互为相反数
赞同
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 米,求
米,求

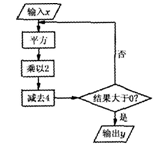
 的解集是 .
的解集是 .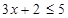 的解集是 .
的解集是 .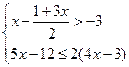 .
.
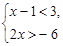 的解集为
的解集为