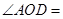题目内容
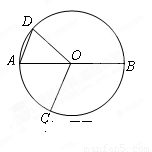
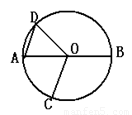
如图,AB是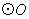 的直径,点C、D在
的直径,点C、D在 上,
上,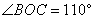 ,
,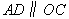 ,则
,则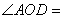 (??? )
(??? )

A.70°?? B.60°?? C.50°?? D.40°
【答案】
D.
【解析】
试题分析:连接BC,由圆周角定理可知∠ACB=90°,由∠BOD=110°可得出∠AOD的度数,根据AC∥OD可知∠CAB=∠AOD,由直角三角形的性质可求出∠ABC的度数,再根据圆周角定理即可得出结论.
连接BC,
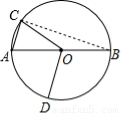
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BOD=110°,
∴∠AOD=180°-110°=70°,
∵AC∥OD,
∴∠CAB=∠AOD=70°,
∵△ABC是直角三角形,
∴∠ABC=90°-∠AOC=90°-70°=20°,
∴∠AOC=2∠ABC=2×20°=40°.
故选D.
考点: 1.圆周角定理;2.平行线的性质;3.等腰三角形的性质.

练习册系列答案
相关题目
如图,AB是 的直径,点C是半圆的中点,动点P在弦BC上,则
的直径,点C是半圆的中点,动点P在弦BC上,则 可能为( )
可能为( )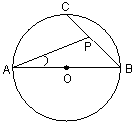
| A.90° | B.50° | C.46° | D.26° |
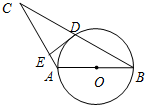 13、如图,AB是的⊙O直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是
13、如图,AB是的⊙O直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是
 的直径,点C、D在
的直径,点C、D在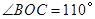 ,
,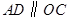 ,则
,则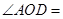 ( )
( )
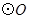 的直径,点C、D在
的直径,点C、D在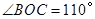 ,
,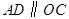 ,则
,则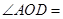
 的直径,点C、D在
的直径,点C、D在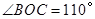 ,
,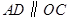 ,则
,则