题目内容
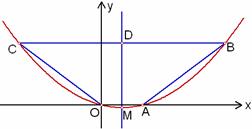
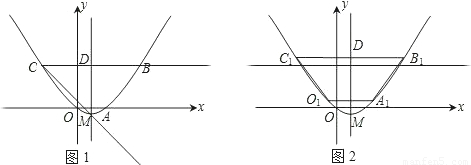
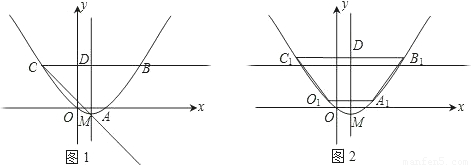
如图1，已知梯形OABC，抛物线分别过点O（0，0）、A（2，0）、B（6，3）．（1）直接写出抛物线的对称轴、解析式及顶点M的坐标；
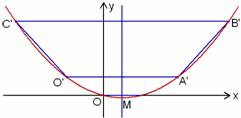
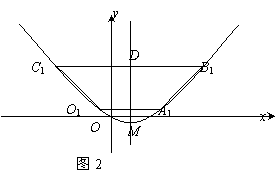
（2）将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移，分别交抛物线于点O1、A1、C1、B1，得到如图2的梯形O1A1B1C1．设梯形O1A1B1C1的面积为S，A1、B1的坐标分别为（x1，y1）、（x2，y2）．用含S的代数式表示x2-x1，并求出当S=36时点A1的坐标；
（3）在图1中，设点D坐标为（1，3），动点P从点B出发，以每秒1个单位长度的速度沿着线段BC运动，动点Q从点D出发，以与点P相同的速度沿着线段DM运动．P、Q两点同时出发，当点Q到达点M时，P、Q两点同时停止运动．设P、Q两点的运动时间为t，是否存在某一时刻t，使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似？若存在，请求出t的值；若不存在，请说明理由．
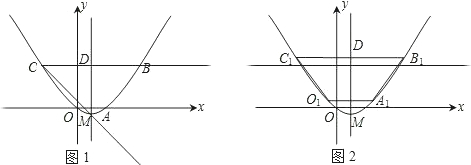
分析：（1）已知了O、A、B的坐标，可用待定系数法求出抛物线的解析式，进而可得到其对称轴方程和顶点M的坐标．
（2）在两条直线平移的过程中，梯形的上下底发生了改变，但是梯形的高没有变化，仍为3，即y2-y1=3，可根据抛物线的解析式，用x1、x2表示出y1、y2，然后联立y2-y1=3，可得到第一个关于x1、x2的关系式①；在两条直线平移过程中，抛物线的对称轴没有变化，可用x1、x2以及抛物线的对称轴解析式表示出梯形上下底的长，进而可得到梯形面积的表达式，这样可得到另外一个x1、x2的关系式②，联立两个关系式，即可得到关于（x2-x1）与S的关系式③，将S=36代入②③的关系式中，即可列方程组求得x1、x2的值，进而可求出A点的坐标．
（3）要解答此题，首先要弄清几个关键点：
一、当PQ∥AB时，设直线AB与抛物线对称轴的交点为E，可得△DPQ∽△DBE，可用t表示出DP、DQ的长，而E点坐标易求得，根据相似三角形所得比例线段，即可得到此时t的值即t=
；
二、当P、Q都停止运动时，显然BC＞DM，所以此时t=DM÷1=3
；
可分两种情况讨论：
①当0＜t＜
时，设直线PQ与直线AB的交点为F，与x轴的交点为G；由题意知△FQE∽△FAG，得∠FGA=∠FEQ，由于BC∥x轴，则∠DPQ=∠FGA=∠FEQ，由此可证得△DPQ∽△DEB，DB、DE的长已求得，可用t表示出DP、DQ的长，根据相似三角形所得比例线段，即可求得此时t的值；
②当
＜t＜3
时，方法同①；
在求得t的值后，还要根据各自的取值范围将不合题意的解舍去．
（2）在两条直线平移的过程中，梯形的上下底发生了改变，但是梯形的高没有变化，仍为3，即y2-y1=3，可根据抛物线的解析式，用x1、x2表示出y1、y2，然后联立y2-y1=3，可得到第一个关于x1、x2的关系式①；在两条直线平移过程中，抛物线的对称轴没有变化，可用x1、x2以及抛物线的对称轴解析式表示出梯形上下底的长，进而可得到梯形面积的表达式，这样可得到另外一个x1、x2的关系式②，联立两个关系式，即可得到关于（x2-x1）与S的关系式③，将S=36代入②③的关系式中，即可列方程组求得x1、x2的值，进而可求出A点的坐标．
（3）要解答此题，首先要弄清几个关键点：
一、当PQ∥AB时，设直线AB与抛物线对称轴的交点为E，可得△DPQ∽△DBE，可用t表示出DP、DQ的长，而E点坐标易求得，根据相似三角形所得比例线段，即可得到此时t的值即t=
| 15 |
| 7 |
二、当P、Q都停止运动时，显然BC＞DM，所以此时t=DM÷1=3
| 1 |
| 8 |
可分两种情况讨论：
①当0＜t＜
| 15 |
| 7 |
②当
| 15 |
| 7 |
| 1 |
| 8 |
在求得t的值后，还要根据各自的取值范围将不合题意的解舍去．
解答：解：（1）对称轴：直线x=1，
解析式：y=
x2-
x，
顶点坐标：M（1，-
）．
（2）由题意得y2-y1=3，y2-y1=
-
x2-
+
x1=3，
得：（x2-x1）[
（x2+x1）-
]=3①，
s=
=3（x1+x2）-6，
得：x1+x2=
+2②，
把②代入①并整理得：x2-x1=
（S＞0），
当s=36时，
，
解得：
，
把x1=6代入抛物线解析式得y1=3，
∴点A1（6，3）．
（3）存在
易知直线AB的解析式为y=
x-
，可得直线AB与对称轴的交点E的坐标为（1，-
），
∴BD=5，DE=
，DP=5-t，DQ=t，
当PQ∥AB时，
=
，
=
，
得t=
，
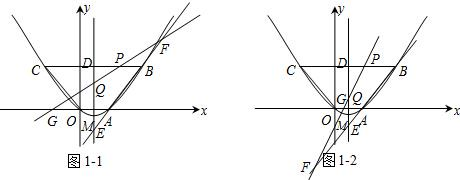
下面分两种情况讨论：设直线PQ与直线AB、x轴的交点分别为点F、G；
①当0＜t＜
时，如图1-1；
∵△FQE∽△FAG，∴∠FGA=∠FEQ，
∴∠DPQ=∠DEB；易得△DPQ∽△DEB，
∴
=
，
∴
=
，
得t=
＞
，
∴t=
（舍去）；
②当
＜t＜3
时，如图1-2；
∵△FQE∽△FAG，
∴∠FAG=∠FQE，
∵∠DQP=∠FQE，∠FAG=∠EBD，
∴∠DQP=∠DBE，易得△DPQ∽△DEB，
∴
=
，
∴
=
，
∴t=
；
∴当t=
秒时，使直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似．
解析式：y=
| 1 |
| 8 |
| 1 |
| 4 |
顶点坐标：M（1，-
| 1 |
| 8 |
（2）由题意得y2-y1=3，y2-y1=
| 1 |
| 8 |
| x | 2 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| x | 2 1 |
| 1 |
| 4 |
得：（x2-x1）[
| 1 |
| 8 |
| 1 |
| 4 |
s=
| 2(x1-1+x2-1)×3 |
| 2 |
得：x1+x2=
| s |
| 3 |
把②代入①并整理得：x2-x1=
| 72 |
| s |
当s=36时，
|
解得：
|
把x1=6代入抛物线解析式得y1=3，
∴点A1（6，3）．
（3）存在
易知直线AB的解析式为y=
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
∴BD=5，DE=
| 15 |
| 4 |
当PQ∥AB时，
| DQ |
| DE |
| DP |
| DB |
| t | ||
|
| 5-t |
| 5 |
得t=
| 15 |
| 7 |
下面分两种情况讨论：设直线PQ与直线AB、x轴的交点分别为点F、G；
①当0＜t＜
| 15 |
| 7 |
∵△FQE∽△FAG，∴∠FGA=∠FEQ，
∴∠DPQ=∠DEB；易得△DPQ∽△DEB，
∴
| DQ |
| DB |
| DP |
| DE |
∴
| t |
| 5 |
| 5-t | ||
|
得t=
| 20 |
| 7 |
| 15 |
| 7 |
∴t=
| 20 |
| 7 |
②当
| 15 |
| 7 |
| 1 |
| 8 |
∵△FQE∽△FAG，
∴∠FAG=∠FQE，
∵∠DQP=∠FQE，∠FAG=∠EBD，
∴∠DQP=∠DBE，易得△DPQ∽△DEB，
∴
| DQ |
| DB |
| DP |
| DE |
∴
| t |
| 5 |
| 5-t | ||
|
∴t=
| 20 |
| 7 |
∴当t=
| 20 |
| 7 |
点评：本题是二次函数的综合类试题，涉及到：二次函数解析式的确定、等腰梯形的性质、图形面积的求法、相似三角形的判定和性质等重要知识；在（3）题中能够正确的画出图形，并准确的找到所求的三角形是解答此题的关键．
练习册系列答案
相关题目
－
，并求出当S=36时点A1的坐标；
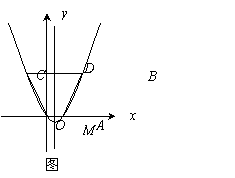（3）在图1中，设点D坐标为(1，3)，动点P从点B出发，以每秒1个单位长度的速度沿着线段BC运动，动点Q从点D出发，以与点P相同的速度沿着线段DM运动．P、Q两点同时出发，当点Q到达点M时，P、Q两点同时停止运动．设P、Q两点的运动时间为t，是否存在某一时刻t，使得直线PQ、直线AB、
轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似？若存在，请求出t的值；若不存在，请说明理由．
